I have chosen Lot C, which I have included in the last picture. Thank you so much to the people that decide to help !

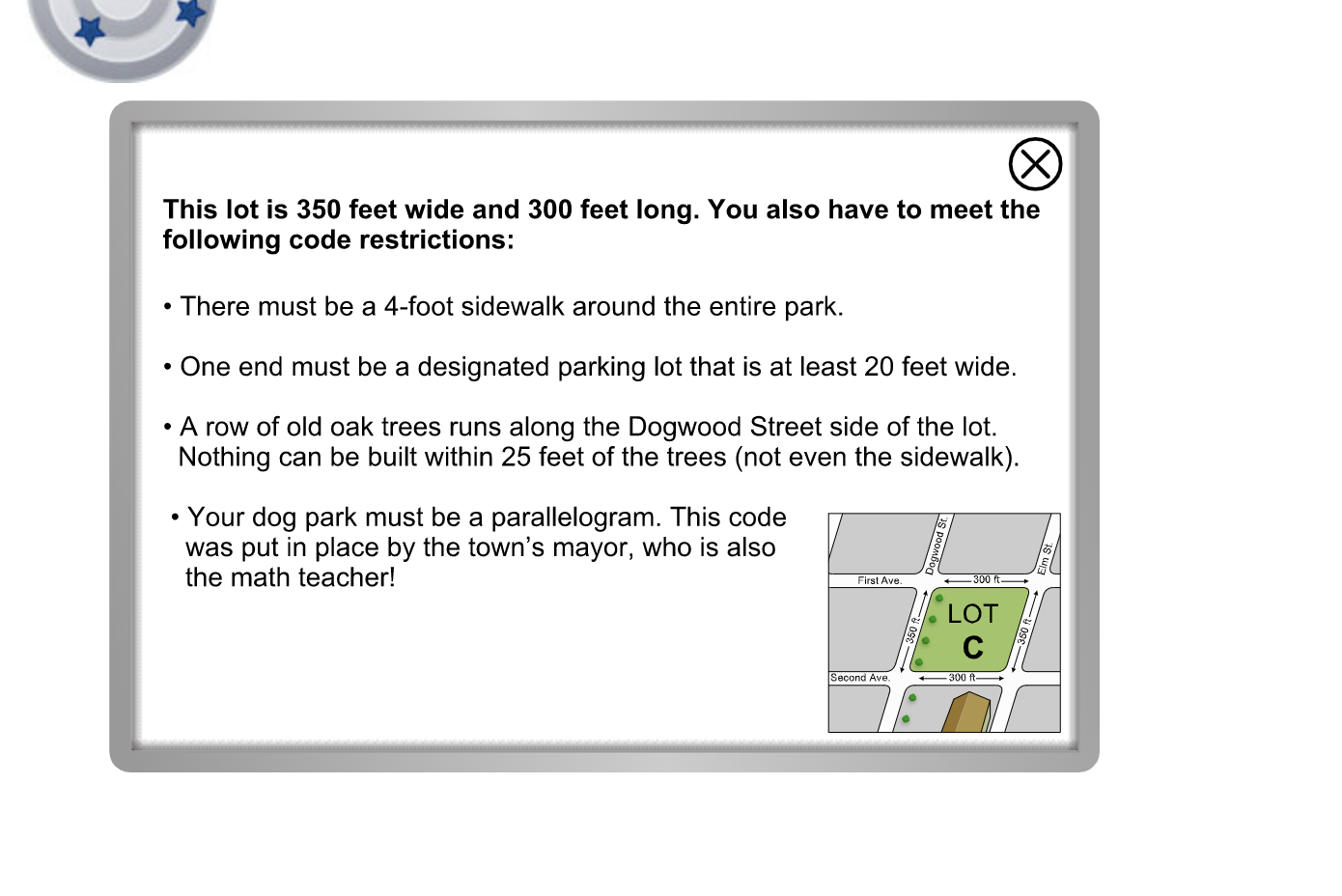
Planning your dog park: 3. Draw a picture that represents what you know about the empty lot. (2 points) 4. Is the empty lot a parallelogram? Why or why not? (2 points) 5. Where are you going to put the parking lot? Draw the parking lot on your map and label its dimensions. (2 points) 6. Is your parking lot a parallelogram? (2 points) 7. Draw in the dimensions of the zone restricted by the creek or trees. (1 point) 8. Draw in the sidewalk and its dimensions. (2 points) Solving the Problem: 9. What are the nal dimensions of the largest dog park you can create on your lot (not including the sidewalk or the parking lot)? Use the Quadrilateral Tool located in the activity to help you. (2 points) 10. Most importantly, to satisfy the mayor, is this space a parallelogram? Why or why not? (1 point) 11. Draw a sketch of your dog park. Correctly label the dimensions that prove your dog park is a parallelogram. (2 points) \f This lot is 350 feet wide and 300 feet long. You also have to meet the following code restrictions: - There must be a 4-foot sidewalk around the entire park. - One end must be a designated parking lot that is at least 20 feet wide. - A row of old oak trees runs along the Dogwood Street side of the lot. Nothing can be built within 25 feet of the trees (not even the sidewalk). . Your dog park must be a parallelogram. This code was put in place by the town's mayor, who is also the math teacher