I have provided the theorem and figure needed for this problem.

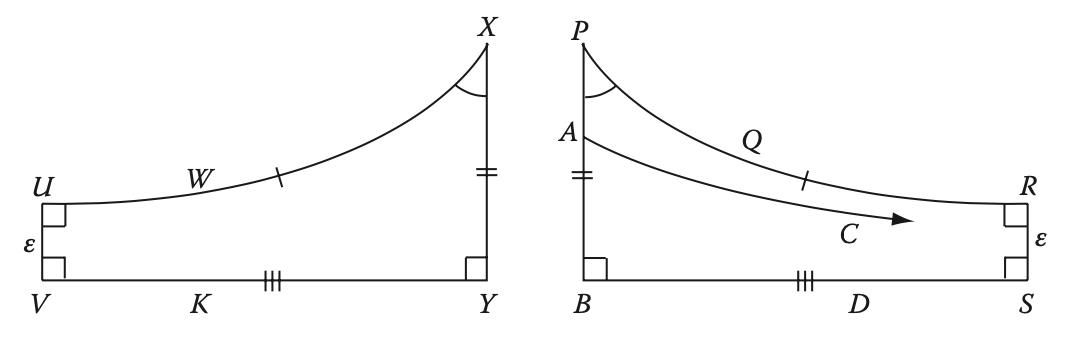
E = Asymptotic Parallelism Let AC || BD, where AB 1 BD, and let be a given positive real. There exists a point X on ray AC such that the perpendicular distance from X to ray BD is less than (i.e., if Y is the foot of X on line BD, as AX , XY 0). The proof is outlined in the following; you are to fill in the details (Figure P.17). 1. Let UV = ; construct rays UW and VK perpendicular to segment UV. Since UW || a VK, there exists a per- pendicular segment XY from ray UW to VK such that XY > AB. (See Problem 16.) 2. Construct P on ray BA such that BP = XY and ray PQ on the C-side of line AB such that ZBPR = ZUXY. Locate R on ray PQ such that PR = XU, and S on ray BD such that BS = VY. Then RS = UV and line RS is the common perpendicular to lines PQ and RS. 3. Since (PAB), ray AC intersects segment RS at an inte- rior point. (Apply the Postulate of Paseh to APBR and use Theorem 2, Section 5.8.) (Figure P.17) = x P A th W # U R E E 1 V K Y B D S Theorem 2 If AAB12 is an asymptotic triangle, and P and Q are any two points lying on lines AC and BD, respectively, then APQA2 is also an asymptotic triangle. E = Asymptotic Parallelism Let AC || BD, where AB 1 BD, and let be a given positive real. There exists a point X on ray AC such that the perpendicular distance from X to ray BD is less than (i.e., if Y is the foot of X on line BD, as AX , XY 0). The proof is outlined in the following; you are to fill in the details (Figure P.17). 1. Let UV = ; construct rays UW and VK perpendicular to segment UV. Since UW || a VK, there exists a per- pendicular segment XY from ray UW to VK such that XY > AB. (See Problem 16.) 2. Construct P on ray BA such that BP = XY and ray PQ on the C-side of line AB such that ZBPR = ZUXY. Locate R on ray PQ such that PR = XU, and S on ray BD such that BS = VY. Then RS = UV and line RS is the common perpendicular to lines PQ and RS. 3. Since (PAB), ray AC intersects segment RS at an inte- rior point. (Apply the Postulate of Paseh to APBR and use Theorem 2, Section 5.8.) (Figure P.17) = x P A th W # U R E E 1 V K Y B D S Theorem 2 If AAB12 is an asymptotic triangle, and P and Q are any two points lying on lines AC and BD, respectively, then APQA2 is also an asymptotic triangle