I have some problems which I did not figure out how to do it in topic "Sampling distribution and the CLT". Please help me, thank you so much!!!!

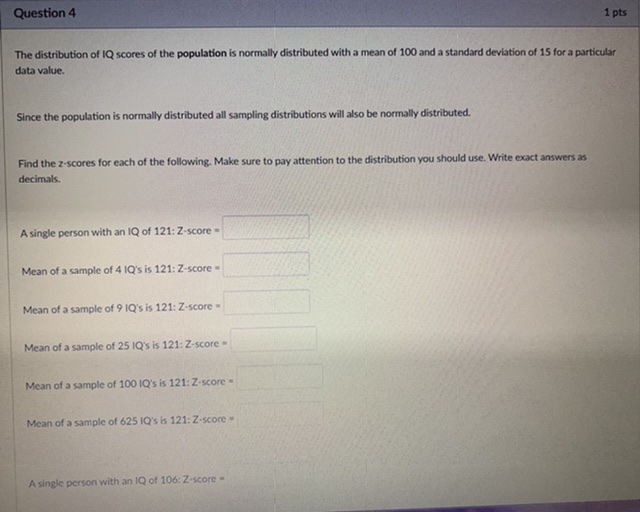
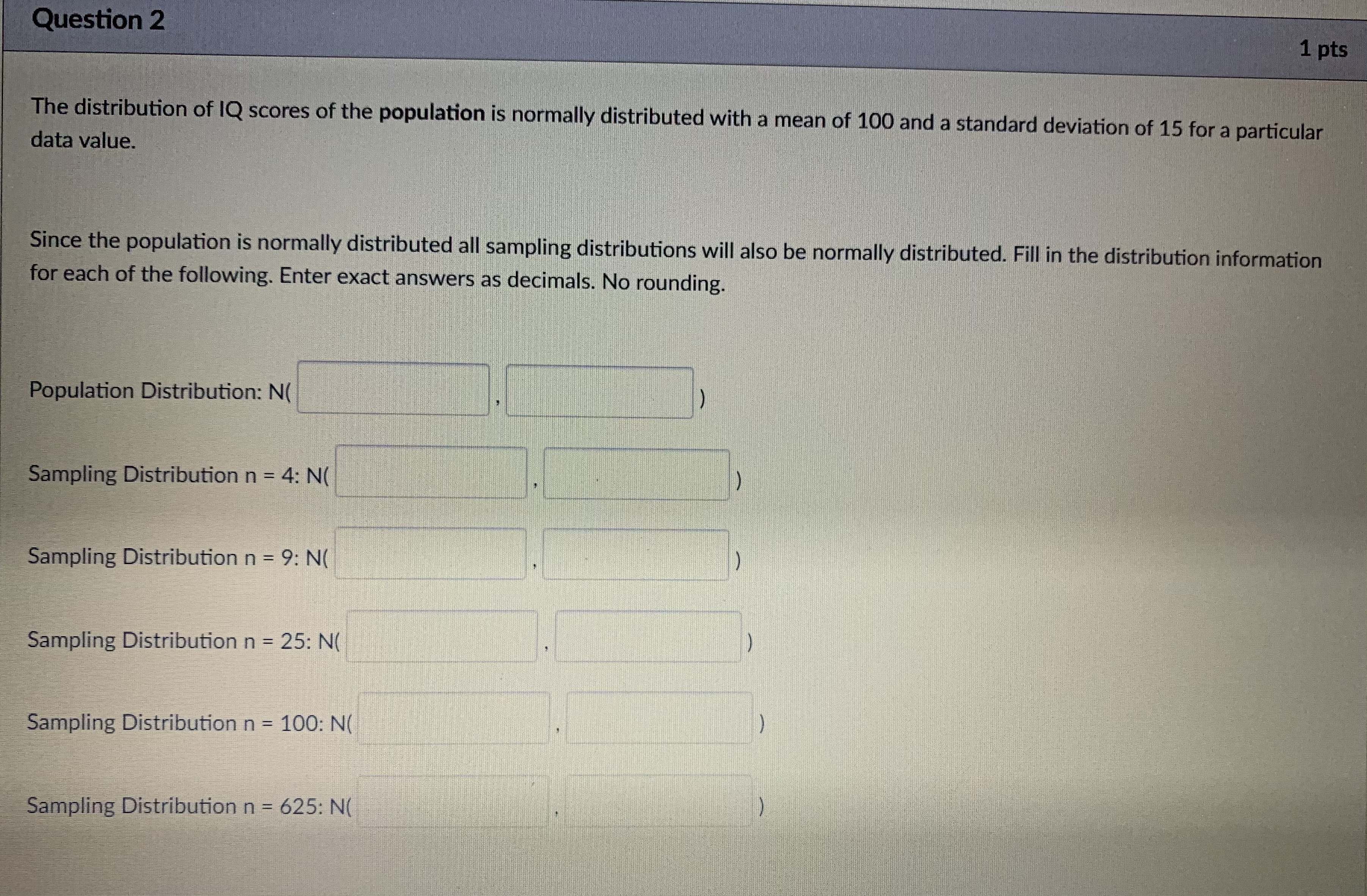
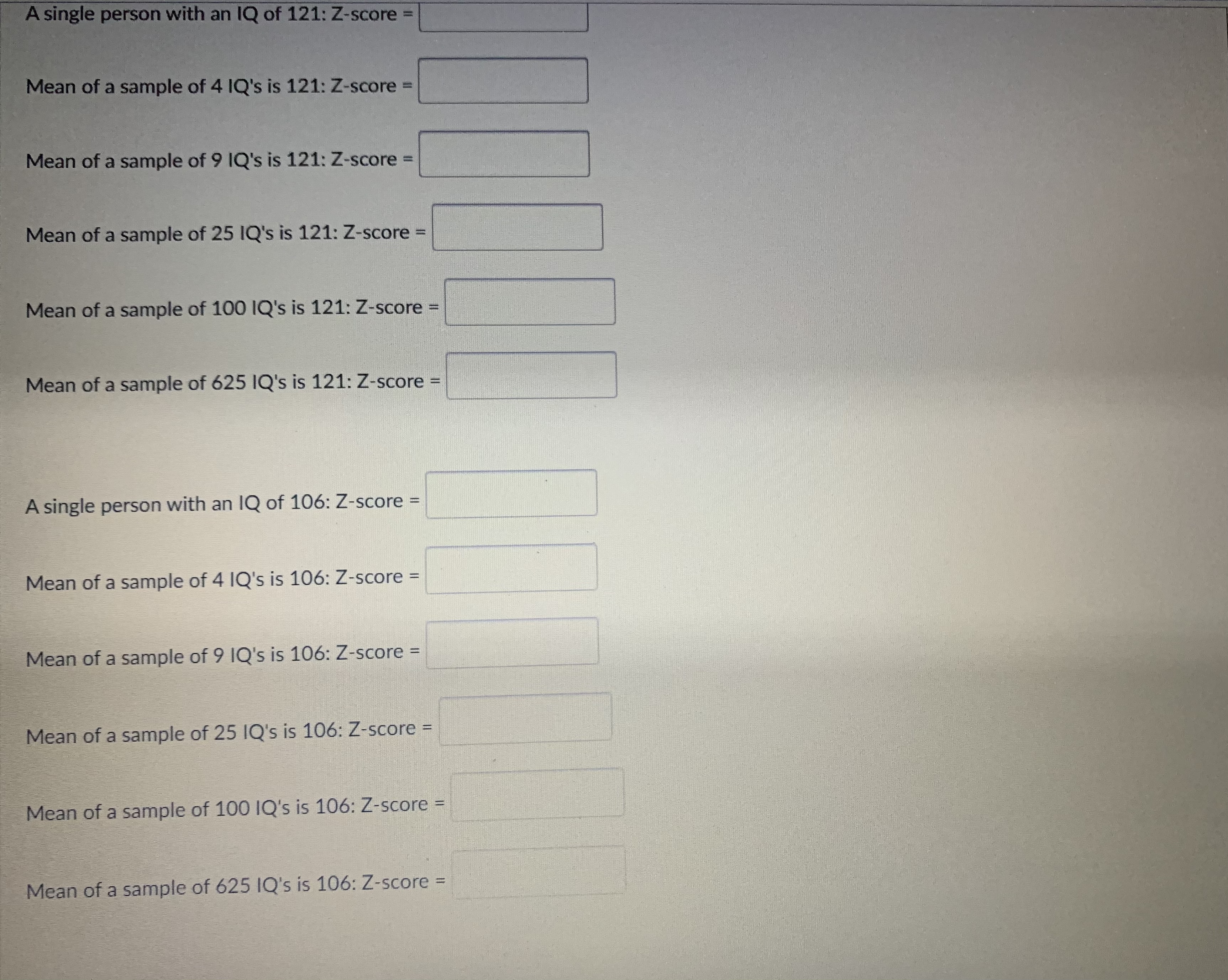
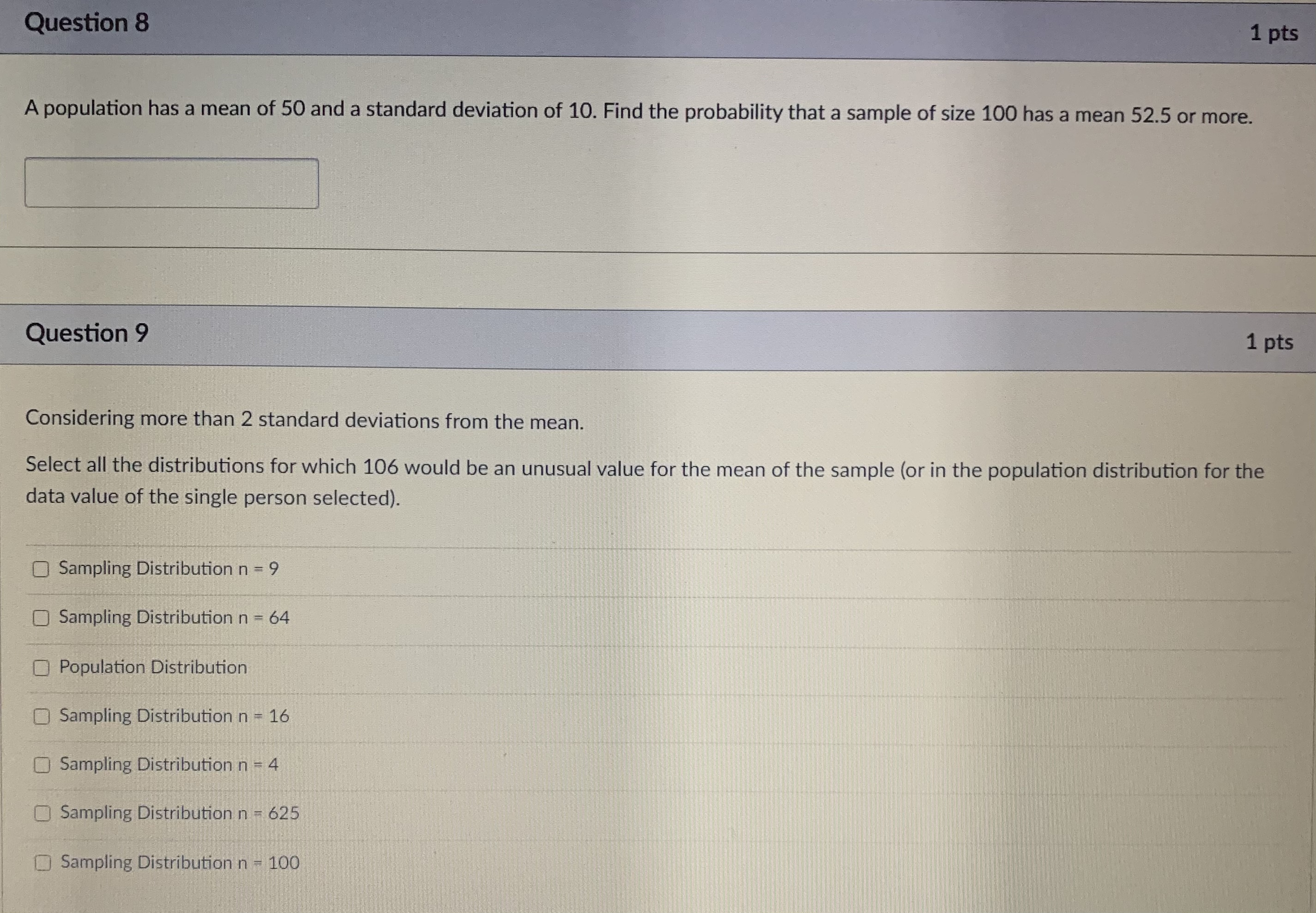
Question 4 1 pts The distribution of IQ scores of the population is normally distributed with a mean of 100 and a standard deviation of 15 for a particular data value. Since the population is normally distributed all sampling distributions will also be normally distributed. Find the z-scores for each of the following. Make sure to pay attention to the distribution you should use. Write exact answers as decimals. A single person with an IQ of 121: Z-score = Mean of a sample of 4 IQ's is 121: Z-score = Mean of a sample of 9 IQ's is 121: Z-score = Mean of a sample of 25 IQ's is 121: Z-score = Mean of a sample of 100 IQ's is 121: Z-score = Mean of a sample of 625 IQ's is 121: Z-score = A single person with an IQ of 106:2-score =Question 10 0.5 pts If X is normally distributed with a mean of 80 and a standard deviation of 8.88. If you take a sample of size 240, what is the mean of the sampling distribution? Write your answer correct to 4 decimal places.Question 2 1 pts The distribution of IQ scores of the population is normally distributed with a mean of 100 and a standard deviation of 15 for a particular data value. Since the population is normally distributed all sampling distributions will also be normally distributed. Fill in the distribution information for each of the following. Enter exact answers as decimals. No rounding. Population Distribution: N( Sampling Distribution n = 4: N( Sampling Distribution n = 9: N( Sampling Distribution n = 25: N( Sampling Distribution n = 100: N( Sampling Distribution n = 625: N(\fQuestion 8 1 pts A population has a mean of 50 and a standard deviation of 10. Find the probability that a sample of size 100 has a mean 52.5 or more. Question 9 1 pts Considering more than 2 standard deviations from the mean. Select all the distributions for which 106 would be an unusual value for the mean of the sample (or in the population distribution for the data value of the single person selected). O Sampling Distribution n = 9 O Sampling Distribution n = 64 Population Distribution Sampling Distribution n = 16 Sampling Distribution n = 4 Sampling Distribution n = 625 Sampling Distribution n - 100