I have written a c code to solve this problem analytically:

#include

double calc_prob(int people)

{

int n=365,i=0;

double sum=1;

for(i=0;i

{

sum=sum*n/365;

n=n-1;

}

return 1-sum;

}

int main()

{

int people;

printf(" Enter how many people are there:");

scanf("%d",&people);

printf(" So Probability that atleast 2 people have same birthday out of %d peo$

return 1;

}

Below is the output for the above, when N=2,3,4 (done analytically)

Now help me with the c code to Generalize this for N persons and compare the result with the Monte Carlo method.

sample: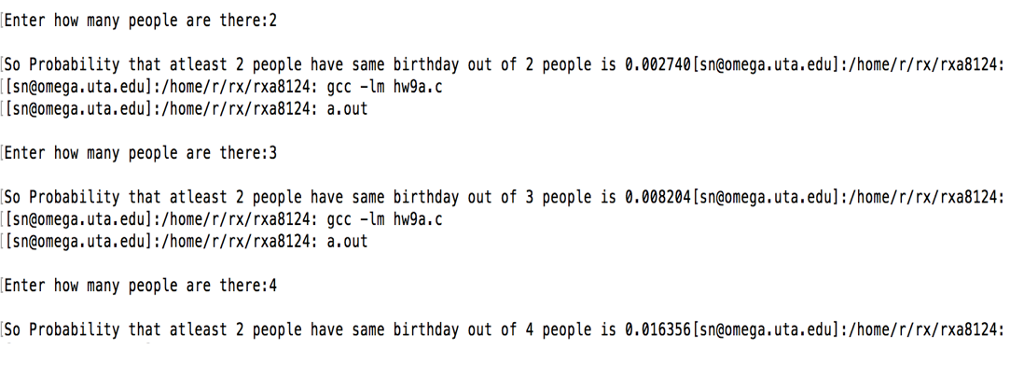

#include  #include  #include  #define n 10000 int main() { int i,j,k,count=0, N; int birthday[100]; printf("Enter # of people =");scanf("%d", &N); srand(time(NULL)); for(k=0;k 
 
  Write C code for the following: 1. (Birthday paradox revisited) Compute analytically the probability that at least two people in a group of N persons have the same birthdav. Hint: Let's say, N = 4 . Then, the number of possible birthday combinations for 4 persons is The number of possible cases where 4 persons have different birthdays (no one shares the same 365 365 x365 x365. birthday) is 365 x364 x363 x362 Therefore, the probability that all 4 persons have different birthdays is 365 364 363 362 365 365 365 365 and the probability that at least two people out of 4 have a same birthday is 365 364 363 362 365 365 365 365 Generalize this for N persons and compare the result with the Monte Carlo method. Monte Carlo C program