$in$ Types ::$=$ nat $|listt({}_1)|arr({}_1$;${}_2)$

ein Exprs ::$=x|z|s(e)|rec\{e_0$;$x.y.e_1\}(e)|nill\{\}|cons(e_1$;$e_2)|lrec\{e_0$; $h.t.y.e_1\}(e)|$

lam$\{\}(x.e)|ap(e_1$;$e_2)$

The statics and dynamics of this system extend that of eager System T$,$ with the following typing rules for the new constructors:

$\frac{?}{\text{b}\text{a}\text{r}}(|--$nill$\{\}$:listt$()),\frac{|--e_1\text{:},|--e_2\text{:}\text{l}\text{i}\text{s}\text{t}\text{t}()}{|--\text{c}\text{o}\text{n}\text{s}(e_1\text{;}{e}_2)\text{:}\text{l}\text{i}\text{s}\text{t}\text{t}()}$

$\frac{|--e_0\text{:},,h\text{:},t\text{:}\text{l}\text{i}\text{s}\text{t}\text{t}(),y\text{:}|--e_1\text{:},|--e\text{:}\text{l}\text{i}\text{s}\text{t}\text{t}()}{|--\text{l}\text{r}\text{e}\text{c}\{e_0\text{;}h.t.y.e_1\}(e)\text{:}}$

The dynamics for lists mirrors that for natural numbers:

nill$\{\}$ is a value,

cons$(e_1$;$e_2)$ is a value if both $e_1$ and $e_2$ are,

evaluation of the arguments of cons is left$-$to$-$right, and

evaluation of lrec$\{e_0$;$h.t.y.e_1\}(e)$ proceeds by first evaluating $e$ until it is a value $--$ either nill $\{\}$ or cons $(e_2$;$e_3)--$ and then

either producing $e_0$ or $[\frac{e_2}{h}][\frac{e_3}{t}][Irec\{e_0$;$h.t.y.e_1\}\frac{e_3}{y}]e_1$ respectively.

You are also to define a big$-$step dynamics for this system using the judgment $ev$ that corresponds to the combination of $elongmapst{o}^{**}v$ and

$v$ val.

In all, the judgment constructors you need to declare in your $.$sig file are of$,$ val, step, steps, and eval.

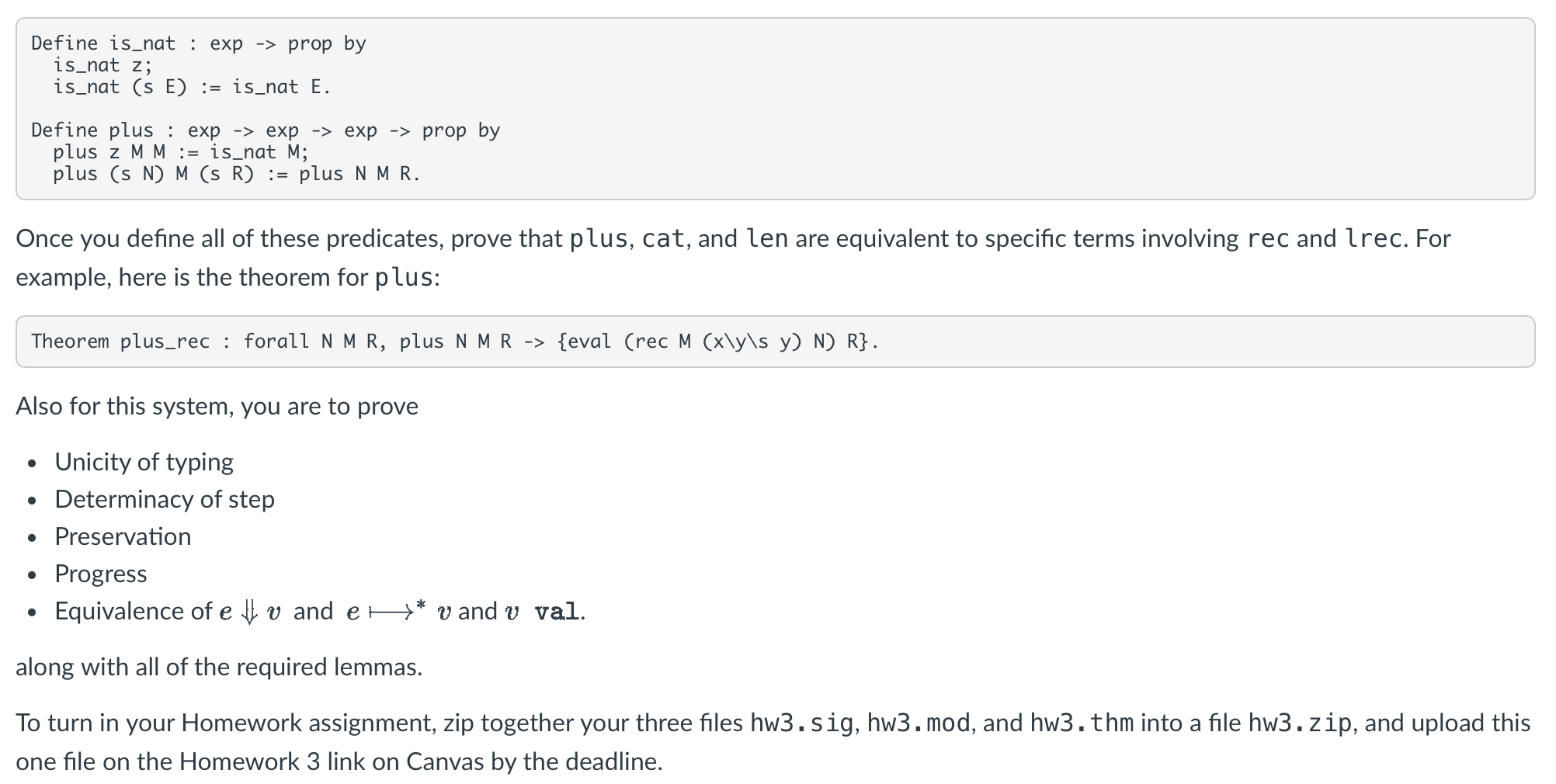
For this system, you are to define predicates $($using Define in the $.$ thm file$)$ is$\_$nat, is$\_$list, plus, times, cat, len, and rev $($reverse$).$

For example, here are definitions for is$\_$nat and plus:

example, here is the theorem for plus:

Also for this system, you are to prove

Unicity of typing

Determinacy of step

Preservation

Progress

Equivalence of $ev$ and $elongmapst{o}^{**}v$ and $v$ val.

along with all of the required lemmas.

To turn in your Homework assignment, zip together your three files hw$3.$sig, hw$3.$ mod, and hw$3.$ thm into a file hw$3.$zip, and upload this

one file on the Homework $3$ link on Canvas by the deadline.