I need a matlab function which:

-defines A(matrix), b(matrix), n(number of equations)

-input: x^(0)=(0,0,0,0,)^T

-call Jacobi (20 iterations)

-store errors (see instructions in pictures)

-call GaussSeidel (20 iterations)

-store errors(see instructions in pictures)

-call SOR (20 iterations)

-store errors(see instructions in pictures)

-print errors (3 columns)

done

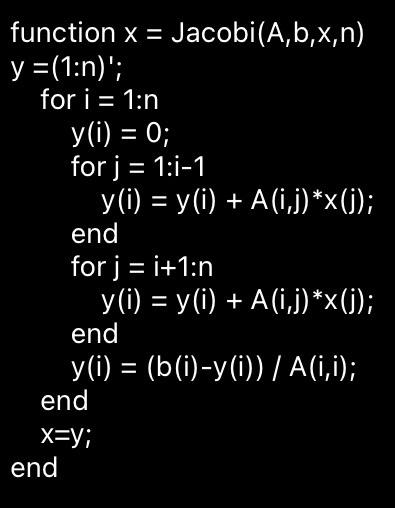
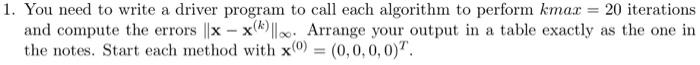
function x = Jacobi(A,b,x,n) y =(1:n)'; for i = 1:n y(i) = 0; for j = 1:1-1 y(i) = y(i) + A(1,j) *x(j); end for j = i+1:n y(i) = y(i) + A(1,j) *x(j); end y(i) = (b(i)-y(i)) / A(1,1); end x=y; end function x = SOR(A,b,x,n,omega) for i = 1:n S = 0; for j = 1:1-1 S = s + A(1,3)*x(j); end for j = i+1:n s=s+ A(1,j) *x(i); end s = (b(i) - s) / A(i,i); x(i) = x(i) + omega*(s - x(i)); end end function x = GaussSeidel(A,b,x,n) for i = 1:n s = 0; for j = 1:1-1 s= s + A(1,j) *x(j); end for j=i+1:n s=s+ A(1,j) *x(j); end x(i) = (b (i) - s) / A(i,i); end end 1. You need to write a driver program to call each algorithm to perform kmax = 20 iterations and compute the errors ||x - x(k) || Arrange your output in a table exactly as the one in the notes. Start each method with x() = (0,0,0,0). function x = Jacobi(A,b,x,n) y =(1:n)'; for i = 1:n y(i) = 0; for j = 1:1-1 y(i) = y(i) + A(1,j) *x(j); end for j = i+1:n y(i) = y(i) + A(1,j) *x(j); end y(i) = (b(i)-y(i)) / A(1,1); end x=y; end function x = SOR(A,b,x,n,omega) for i = 1:n S = 0; for j = 1:1-1 S = s + A(1,3)*x(j); end for j = i+1:n s=s+ A(1,j) *x(i); end s = (b(i) - s) / A(i,i); x(i) = x(i) + omega*(s - x(i)); end end function x = GaussSeidel(A,b,x,n) for i = 1:n s = 0; for j = 1:1-1 s= s + A(1,j) *x(j); end for j=i+1:n s=s+ A(1,j) *x(j); end x(i) = (b (i) - s) / A(i,i); end end 1. You need to write a driver program to call each algorithm to perform kmax = 20 iterations and compute the errors ||x - x(k) || Arrange your output in a table exactly as the one in the notes. Start each method with x() = (0,0,0,0)