i need a solution answer for this report plz for Determining Enthalpy of Vaporization Using Vapor Pressure

all the required data are below

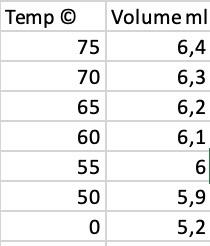
Determining Enthalpy of Vaporization Using Vapor Pressure Obicetive- To determine the enthalpy of vaporization of water using the Clausius-Clapeyron equation. Back Ground Information- In the experiment you will determine the vapor pressure of a liquid at various temperatures. Vapor pressure is an intensive property, which means it is independent of quantity. This property does change with temperature, the higher the temperature, the greater the vapor pressure. There are several ways to determine vapor pressure. Since, boiling occurs when vapor pressure equals atmospheric pressure. You could change the atmospheric pressure and observe the temperature which a liquid boils. Lowering the pressure lowers the boiling point. This is too easy. Actually we do not have the equipment to determine the vapor pressure this way. This experiment will use a small amount of air trapped in an inverted 10.0mL graduated cylinder immersed in a beaker of water. The water temperature will range from 75.0C down to 50.0C and then lowered to 0.0C by adding a large quantity of ice to the beaker. As the water bath cools, the temperature and volume of the gas will be recorded every 5.0C. In order to minimize the error, the measuring of the volume of gas should only be made if the pressure inside the graduated cylinder and the atmosphere are equal. The graduated cylinder will be raise to allow the water level inside the cylinder and the water bath to be equal. The pressure inside the cylinder and outside the cylinder will be equal. Only then can the volume of the gas inside be measurod. The most crucial measurement for this experiment is the 0.0C, where the assumed vapor pressure of water is zero. Any error measuring here will cause an enormous error later in the lab. The Clausius Clapeyron Equation is a mathematical relationship relating the vapor pressure of a liquid to the temperature of the liquid. When vapor pressure is plotted against temperature, a nonlinear trend is observed, as shown in figure 1. We find that a straight line can be obtained by plotting ln(Pxay) versus 1/T, where T is the Kelvin temperature as shown in figure 2 . Prosedert: Day 1 the bot plate to the bighet sething and allow the witer to boll. Room wonperatise waker 2. Ter edf te het plate and pever the beaker with a shect of paper. Day 2 1. Fill 110.0mL grideated clinder with 10mL, of waler. Cover the top of be gratuaned eylinder with you finger, invert the cylinder and vibmerse in in the 600ml beaker of sater. Remeve fitgo and then monove your hasd, leaving the gratuabed cylinser tanding cpside dows in the weer. 4. Ramove the protective stouh from the thermoneter. Clamp the clanp to the blemnometer. Allash the clamp w the ring vamd. Lower be themonecer inve the water Eigure 1 Fipure 2 bah. Do not lat be electrieal bouing of the thermomeder etect the wane, Tem on We con represent dis behavier of Figure 2 by the sumbion 1. Ahermometer. 5. Ten on the bol plaie and beat the water io a iemperecure of 79C. Tum off hat plate. lnP=THq+C Make wre that the vodame of gat does aot apand past of paduation an the zudaded cvlinder. Eqaation 1 6. Sustieg in 75.0C ropord the voluine of air trapped in the splinker when the prosures are equaliead when the water level in the cytinder and the weter bath are at the aame fevel. 7. Oece you reosd the go orC reidisg, ibl ior to fle water in the bedi to bring be beaker to an clacie to 0.0C. Recedil the equalined volame of the gat. miromhip the vilue of ite initulpy of vaperintion can be deermited Y=inPinM=slepe=+Ml.e.kX=1/T(K+)B-aterepeC Calculatiens: cytuden. Hu= = PVIRT "*s Calculation 2-4 should be performed usiog Mictoiof escel, or another . Mresisheet progran. 2. Ueing the moles of "Dry" air determine the purtial presurt of art it the cyliader at tach iemperahire. PermentrRT 3. Sisce the pressure in the cylinder was equalized with the atmophere befoet medauring, we can defermine the prevure forn the water vapor by uiblacting the ealculubod pessure of the dry air tom the atmospheric pessere: Pand=PmanPir 4. Plat a griph of In Prip va. I/T. Uaing the trend-line function, find the slope of be beat fit line. Aleo record R2, which indicates how close the data ia to the siraighe best fit lise. R2 equal to t.00 is a straight line. Deviationa from this indicates poor quality itatin 5. Waing the alope calculate the enahalipy of raporivation. Allvici4Hxshofe Qerithas: 1. What was the Wero of your esperimeet? slluap if water is 4965kJ mol l1, What ean be possike reines fie the ctsce? extain the defferpte between the bed of vaperieatien ef wace tad hesase. 3. Compare ile meuka ia bleal and wat cane where tor theorecal valua mre cakculaid frem Van de Waslu equetions of vaie \begin{tabular}{|r|r|} Temp c) & Volume ml \\ \hline 75 & 6,4 \\ \hline 70 & 6,3 \\ \hline 65 & 6,2 \\ \hline 60 & 6,1 \\ \hline 55 & 6 \\ \hline 50 & 5,9 \\ \hline 0 & 5,2 \\ \hline \end{tabular} For example; You can compare your results by doing the same calculations by using other equations of state. For example; For van der waals equation of state; You can use this equations, (p+V2n2a)(Vnb)=nRT atm liter 2/mol2,b=0.0366L/mol for air, you should select R gas constant according to these units. You should use excell and you can use goal seek option to make the necessary calculations. Determining Enthalpy of Vaporization Using Vapor Pressure Obicetive- To determine the enthalpy of vaporization of water using the Clausius-Clapeyron equation. Back Ground Information- In the experiment you will determine the vapor pressure of a liquid at various temperatures. Vapor pressure is an intensive property, which means it is independent of quantity. This property does change with temperature, the higher the temperature, the greater the vapor pressure. There are several ways to determine vapor pressure. Since, boiling occurs when vapor pressure equals atmospheric pressure. You could change the atmospheric pressure and observe the temperature which a liquid boils. Lowering the pressure lowers the boiling point. This is too easy. Actually we do not have the equipment to determine the vapor pressure this way. This experiment will use a small amount of air trapped in an inverted 10.0mL graduated cylinder immersed in a beaker of water. The water temperature will range from 75.0C down to 50.0C and then lowered to 0.0C by adding a large quantity of ice to the beaker. As the water bath cools, the temperature and volume of the gas will be recorded every 5.0C. In order to minimize the error, the measuring of the volume of gas should only be made if the pressure inside the graduated cylinder and the atmosphere are equal. The graduated cylinder will be raise to allow the water level inside the cylinder and the water bath to be equal. The pressure inside the cylinder and outside the cylinder will be equal. Only then can the volume of the gas inside be measurod. The most crucial measurement for this experiment is the 0.0C, where the assumed vapor pressure of water is zero. Any error measuring here will cause an enormous error later in the lab. The Clausius Clapeyron Equation is a mathematical relationship relating the vapor pressure of a liquid to the temperature of the liquid. When vapor pressure is plotted against temperature, a nonlinear trend is observed, as shown in figure 1. We find that a straight line can be obtained by plotting ln(Pxay) versus 1/T, where T is the Kelvin temperature as shown in figure 2 . Prosedert: Day 1 the bot plate to the bighet sething and allow the witer to boll. Room wonperatise waker 2. Ter edf te het plate and pever the beaker with a shect of paper. Day 2 1. Fill 110.0mL grideated clinder with 10mL, of waler. Cover the top of be gratuaned eylinder with you finger, invert the cylinder and vibmerse in in the 600ml beaker of sater. Remeve fitgo and then monove your hasd, leaving the gratuabed cylinser tanding cpside dows in the weer. 4. Ramove the protective stouh from the thermoneter. Clamp the clanp to the blemnometer. Allash the clamp w the ring vamd. Lower be themonecer inve the water Eigure 1 Fipure 2 bah. Do not lat be electrieal bouing of the thermomeder etect the wane, Tem on We con represent dis behavier of Figure 2 by the sumbion 1. Ahermometer. 5. Ten on the bol plaie and beat the water io a iemperecure of 79C. Tum off hat plate. lnP=THq+C Make wre that the vodame of gat does aot apand past of paduation an the zudaded cvlinder. Eqaation 1 6. Sustieg in 75.0C ropord the voluine of air trapped in the splinker when the prosures are equaliead when the water level in the cytinder and the weter bath are at the aame fevel. 7. Oece you reosd the go orC reidisg, ibl ior to fle water in the bedi to bring be beaker to an clacie to 0.0C. Recedil the equalined volame of the gat. miromhip the vilue of ite initulpy of vaperintion can be deermited Y=inPinM=slepe=+Ml.e.kX=1/T(K+)B-aterepeC Calculatiens: cytuden. Hu= = PVIRT "*s Calculation 2-4 should be performed usiog Mictoiof escel, or another . Mresisheet progran. 2. Ueing the moles of "Dry" air determine the purtial presurt of art it the cyliader at tach iemperahire. PermentrRT 3. Sisce the pressure in the cylinder was equalized with the atmophere befoet medauring, we can defermine the prevure forn the water vapor by uiblacting the ealculubod pessure of the dry air tom the atmospheric pessere: Pand=PmanPir 4. Plat a griph of In Prip va. I/T. Uaing the trend-line function, find the slope of be beat fit line. Aleo record R2, which indicates how close the data ia to the siraighe best fit lise. R2 equal to t.00 is a straight line. Deviationa from this indicates poor quality itatin 5. Waing the alope calculate the enahalipy of raporivation. Allvici4Hxshofe Qerithas: 1. What was the Wero of your esperimeet? slluap if water is 4965kJ mol l1, What ean be possike reines fie the ctsce? extain the defferpte between the bed of vaperieatien ef wace tad hesase. 3. Compare ile meuka ia bleal and wat cane where tor theorecal valua mre cakculaid frem Van de Waslu equetions of vaie \begin{tabular}{|r|r|} Temp c) & Volume ml \\ \hline 75 & 6,4 \\ \hline 70 & 6,3 \\ \hline 65 & 6,2 \\ \hline 60 & 6,1 \\ \hline 55 & 6 \\ \hline 50 & 5,9 \\ \hline 0 & 5,2 \\ \hline \end{tabular} For example; You can compare your results by doing the same calculations by using other equations of state. For example; For van der waals equation of state; You can use this equations, (p+V2n2a)(Vnb)=nRT atm liter 2/mol2,b=0.0366L/mol for air, you should select R gas constant according to these units. You should use excell and you can use goal seek option to make the necessary calculations