I need answer for question 5. I have attached the previous question and answers to both questions for reference. please provide step wise solution of ques 5

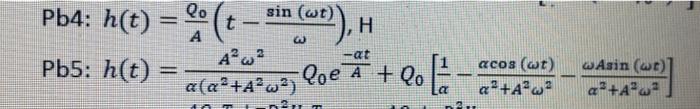
Problem4 A small river stream flows into a large reservoir and fills it with water. We will assume that the reservoir is cylindrical with a cross sectional area A and height H. The flow in the stream varies with the seasons and you propose to model it with a sinusoidal function of the form qi(t)=Q0[1cos(t)](m3/s). Use conservation laws to determine the expression of the variation with time of the level of water in the reservoir; h(t). Assume that the reservoir is initially empty at the dry season. What will be the level of water in the reservoir at very long time (t) ? Problem5 Reconsider the previous problem of flow in a water reservoir. In order to control the level of water in the reservoir, and avoid overflow that may flood the surrounding areas, a pump is used to remove water from the reservoir. An automatic control valve coupled with a sensor allows to adjust the output flow rate by the pump such that it varies with the level of water in the reservoir; qo" .h(t) where has units of m2/s. Determine how the level of water varies when the pump is used. Assume again that the reservoir is initially empty. Pb4:h(t)=AQ0(tsin(t)),H Pb5: h(t)=(2+A22)A22Q0eAt+Q0[12+A22cos(t)2+A22Assin(t)]