I need help coding in python for Machine learning:

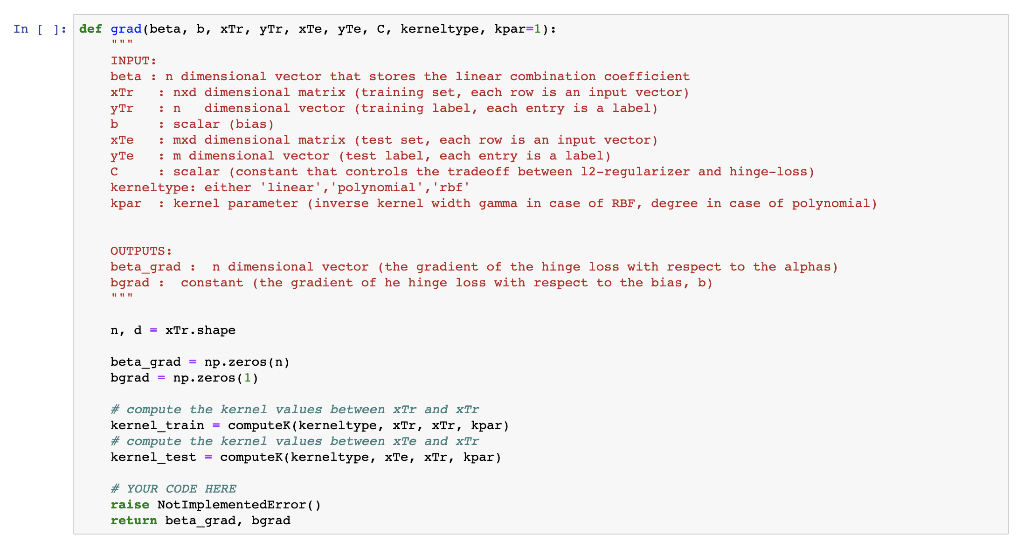def grad(beta, b, xTr, yTr, xTe, yTe, C, kerneltype, kpar=1): """ INPUT: beta : n dimensional vector that stores the linear combination coefficient xTr : nxd dimensional matrix (training set, each row is an input vector) yTr : n dimensional vector (training label, each entry is a label) b : scalar (bias) xTe : mxd dimensional matrix (test set, each row is an input vector) yTe : m dimensional vector (test label, each entry is a label) C : scalar (constant that controls the tradeoff between l2-regularizer and hinge-loss) kerneltype: either 'linear','polynomial','rbf' kpar : kernel parameter (inverse kernel width gamma in case of RBF, degree in case of polynomial) OUTPUTS: beta_grad : n dimensional vector (the gradient of the hinge loss with respect to the alphas) bgrad : constant (the gradient of he hinge loss with respect to the bias, b) """ n, d = xTr.shape beta_grad = np.zeros(n) bgrad = np.zeros(1) # compute the kernel values between xTr and xTr kernel_train = computeK(kerneltype, xTr, xTr, kpar) # compute the kernel values between xTe and xTr kernel_test = computeK(kerneltype, xTe, xTr, kpar) # YOUR CODE HERE raise NotImplementedError() return beta_grad, bgrad

**TESTS**

# These tests test whether your grad() is implemented correctly

xTr_test, yTr_test = generate_data() n, d = xTr_test.shape

# Checks whether grad returns a tuple def grad_test1(): beta = np.random.rand(n) b = np.random.rand(1) out = grad(beta, b, xTr_test, yTr_test, xTr_test, yTr_test, 10, 'rbf') return len(out) == 2

# Checks the dimension of gradients def grad_test2(): beta = np.random.rand(n) b = np.random.rand(1) beta_grad, bgrad = grad(beta, b, xTr_test, yTr_test, xTr_test, yTr_test, 10, 'rbf') return len(beta_grad) == n and np.isscalar(bgrad)

# Checks the gradient of the l2 regularizer def grad_test3(): beta = np.random.rand(n) b = np.random.rand(1) beta_grad, bgrad = grad(beta, b, xTr_test, yTr_test, xTr_test, yTr_test, 0, 'rbf') beta_grad_grader, bgrad_grader = grad_grader(beta, b, xTr_test, yTr_test, xTr_test, yTr_test, 0, 'rbf') return (np.linalg.norm(beta_grad - beta_grad_grader)

# Checks the gradient of the square hinge loss def grad_test4(): beta = np.zeros(n) b = np.random.rand(1) beta_grad, bgrad = grad(beta, b, xTr_test, yTr_test, xTr_test, yTr_test, 1, 'rbf') beta_grad_grader, bgrad_grader = grad_grader(beta, b, xTr_test, yTr_test, xTr_test, yTr_test, 1, 'rbf') return (np.linalg.norm(beta_grad - beta_grad_grader)

# Checks the gradient of the loss def grad_test5(): beta = np.random.rand(n) b = np.random.rand(1) beta_grad, bgrad = grad(beta, b, xTr_test, yTr_test, xTr_test, yTr_test, 10, 'rbf') beta_grad_grader, bgrad_grader = grad_grader(beta, b, xTr_test, yTr_test, xTr_test, yTr_test, 10, 'rbf') return (np.linalg.norm(beta_grad - beta_grad_grader)

runtest(grad_test1, 'grad_test1') runtest(grad_test2, 'grad_test2') runtest(grad_test3, 'grad_test3') runtest(grad_test4, 'grad_test4') runtest(grad_test5, 'grad_test5')

Part Three: Compute Gradient [Graded] Now, you will need to implement function grad , that computes the gradient of the loss function, similarly to what you needed to do in the Linear SVM project. This function has the same input parameters as loss and requires the gradient with respect to B ( beta_grad ) and b ( bgrad ). Remember that the squared hinge loss is calculated with Ktrain when training, and Ktest when testing. In the code, you can represent this by using the variables associated with testing (i.e. xTe , yte , and k_test ), since they will contain training data if you are training the SVM. n Recall the expression for loss from above. First we take the derivative with respect to B: 2KtrainB + c 2 max [1 vi(Ktest[i] + b),o] (-y; Ktest[i]) Then, with respect to b: aL =C X 2 max [1 yi(B+ Kest[i] + b),o] (-y;) Sb i=1 n i=1 In [ ]: def grad(beta, b, xTr, ytr, xTe, yte, C, kerneltype, kpar=1): INPUT: beta : n dimensional vector that stores the linear combination coefficient xTr : nxd dimensional matrix (training set, each row is an input vector) yTr dimensional vector (training label, each entry is a label) : scalar (bias) xTe : mxd dimensional matrix (test set, each row is an input vector) : m dimensional vector (test label, each entry is a label) : scalar (constant that controls the tradeoff between 12-regularizer and hinge-loss) kerneltype: either 'linear', 'polynomial', 'rb' kpar : kernel parameter (inverse kernel width gamma in case of RBF, degree in case of polynomial) OUTPUTS: beta_grad : n dimensional vector (the gradient of the hinge loss with respect to the alphas) bgrad : constant (the gradient of he hinge loss with respect to the bias, b) n, d - xTr.shape beta_grad - np.zeros(n) bgrad = np.zeros(1) # compute the kernel values between xtr and xtr kernel_train - computek (kerneltype, xtr, xTr, kpar) # compute the kernel values between xTe and xTr kernel_test = computek(kerneltype, xTe, xTr, kpar) # YOUR CODE HERE raise Not ImplementedError() return beta_grad, bgrad Part Three: Compute Gradient [Graded] Now, you will need to implement function grad , that computes the gradient of the loss function, similarly to what you needed to do in the Linear SVM project. This function has the same input parameters as loss and requires the gradient with respect to B ( beta_grad ) and b ( bgrad ). Remember that the squared hinge loss is calculated with Ktrain when training, and Ktest when testing. In the code, you can represent this by using the variables associated with testing (i.e. xTe , yte , and k_test ), since they will contain training data if you are training the SVM. n Recall the expression for loss from above. First we take the derivative with respect to B: 2KtrainB + c 2 max [1 vi(Ktest[i] + b),o] (-y; Ktest[i]) Then, with respect to b: aL =C X 2 max [1 yi(B+ Kest[i] + b),o] (-y;) Sb i=1 n i=1 In [ ]: def grad(beta, b, xTr, ytr, xTe, yte, C, kerneltype, kpar=1): INPUT: beta : n dimensional vector that stores the linear combination coefficient xTr : nxd dimensional matrix (training set, each row is an input vector) yTr dimensional vector (training label, each entry is a label) : scalar (bias) xTe : mxd dimensional matrix (test set, each row is an input vector) : m dimensional vector (test label, each entry is a label) : scalar (constant that controls the tradeoff between 12-regularizer and hinge-loss) kerneltype: either 'linear', 'polynomial', 'rb' kpar : kernel parameter (inverse kernel width gamma in case of RBF, degree in case of polynomial) OUTPUTS: beta_grad : n dimensional vector (the gradient of the hinge loss with respect to the alphas) bgrad : constant (the gradient of he hinge loss with respect to the bias, b) n, d - xTr.shape beta_grad - np.zeros(n) bgrad = np.zeros(1) # compute the kernel values between xtr and xtr kernel_train - computek (kerneltype, xtr, xTr, kpar) # compute the kernel values between xTe and xTr kernel_test = computek(kerneltype, xTe, xTr, kpar) # YOUR CODE HERE raise Not ImplementedError() return beta_grad, bgrad