I need help! !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

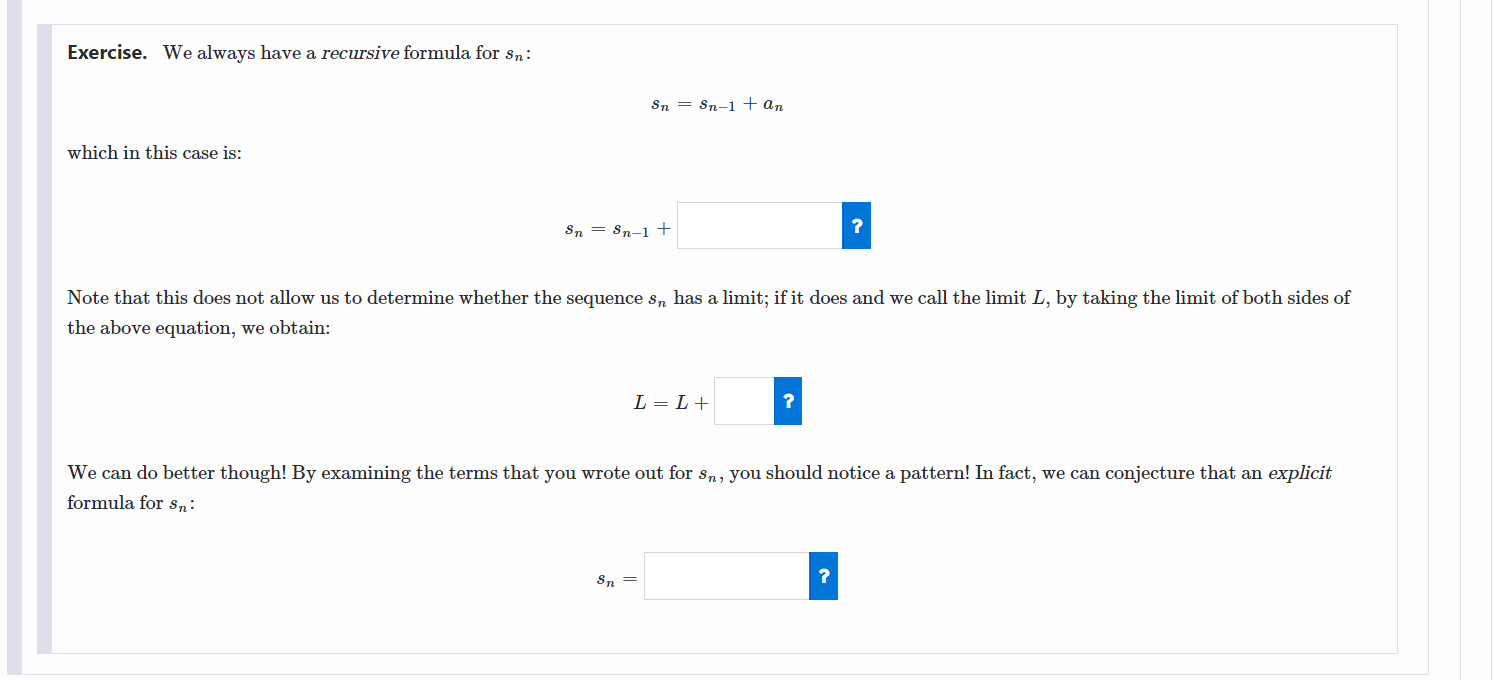
Exercise. We always have a recursive formula for 5": 3n = sn1 + an Which in this case is: 5,, = 3,1,1 + a Note that this does not allow us to determine Whether the sequence 5,, has a limit; if it does and we call the limit L, by taking the limit of both sides of the above equation, we obtain: L = L + I We can do better though! By examining the terms that you wrote out for 3,, , you should notice a pattern! In fact, we can conjecture that an explicit 3n: a formula for s": Exercise. Consider the series: 2 P +K To determine whether the series converges or diverges, complete the following argument: The first step to try to determine if a series " , ak converges is to consider the sequence of partial sums, defined by sn = >;_1 ak = a1 +... + an for n 2 1, and to try to find an explicit formula for sn . To do this, start by finding the partial fraction decomposition of the summand: 2 -2 2 k2 + k k k + 1 Exercise. Write out the first several terms in the sequence {an}n-1 using the partial fraction decomposition above: a1 = 2 a2 = 1 V 2/3 a3 =2 2/3 V 1/2 Q4 = 1/2 V 2/5 V a5 = 2/5 V 1/3 V Exercise. Find $1, $2, $3, $4, and $5 . Pay attention for convenient cancellation! S1 = 2 V S2 = 2 V 2/3 S3 = 2 1/2 S4 = 2 2/5 $5 = 2 V 1/3 V Exercise. We always have a recursive formula for sn