I need help in figuring out how to solve this problem.

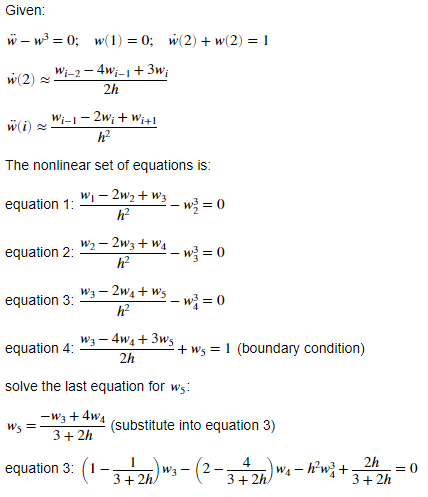
26. Consider the nonlinear BVP with mixed boundary conditions w-w =0, w(1) =0, wix(2)+ w>(2) =1 a. Solve by finite-difference method with Af = 0.25. Use central-difference formula for the second-order derivative, and approximate the first-order derivative in the right boundary condition by a three-point backward-difference formula. Solve the ensuing nonlinear system of equations via Newton's method with all initial values set to 1, and kmax = 10, and tol = 10-4.Given: w - w=0; w(1) =0; w(2) + w(2) =1 w(2) ~ Wi-2 - 4wil + 3w; 2h w(i) ~ - Wi-1 - 2wit WitI h2 The nonlinear set of equations is: equation 1: WI -2w2 + W3 h2 equation 2: W2 - 2w3 + WA h2 equation 3: w3 - 2wat Ws _ 13=0 h2 equation 4: W3 - 4wa + 3ws 2h + wa = 1 (boundary condition) solve the last equation for ws: -Wa + 4wa W5 3+ 2h (substitute into equation 3) equation 3: Wa - 2 4 wit 2h WA - hwa. = 0 3 + 2h 3+ 2h 3+2h