I need help in figuring out the problems for my homework starting from question A-F. I have the answers but I need to know how to workout these problems, any help is greatly appreciated.

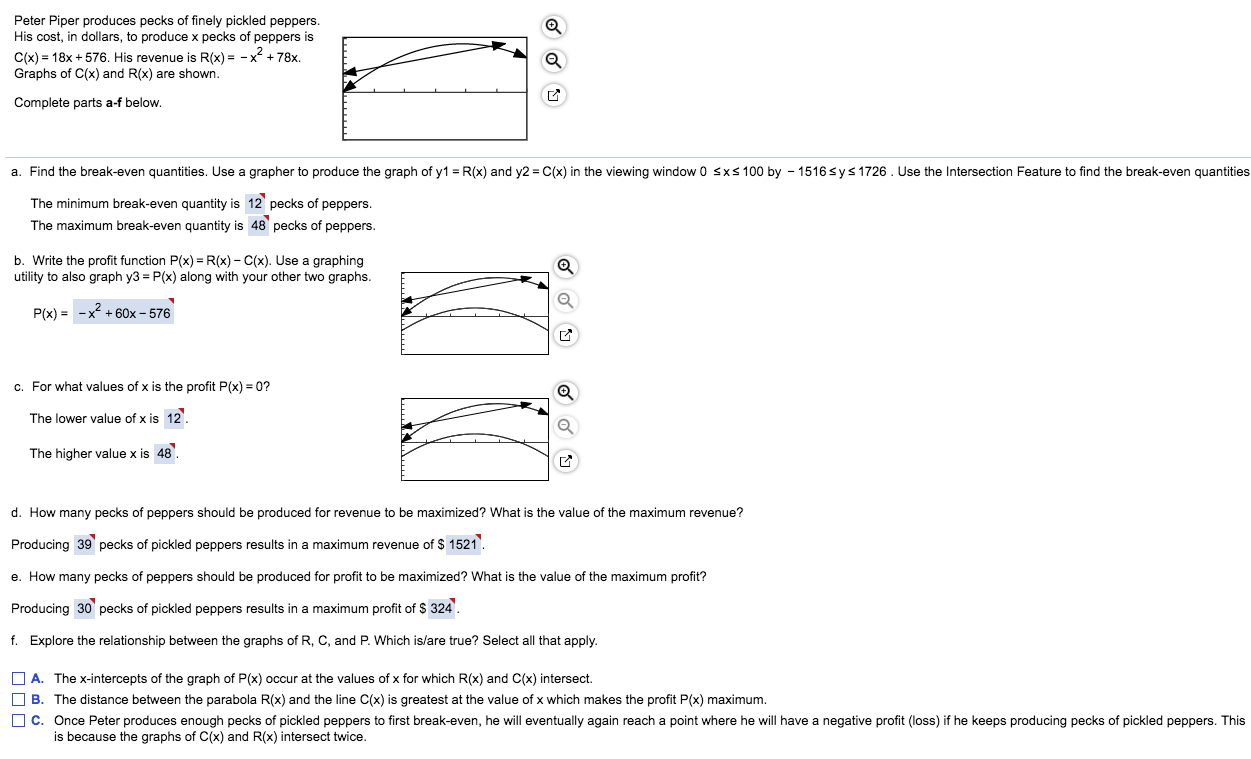
Peter Piper produces pedts ofner piclded peppers. His cost, in dollars, to produce it pecks oi peppers is 9' C(x)=18x +5rs. His revenue is Rix) = x2 + rax. 'll Q Graphs ofCx] and Rh!) are shown. Pp" , comm-ts parts a-f below. - D a. Find the breakeven quanties. Use a glapher to produce the graph ofy1 = R(x} and y2 = C(x} in the viewing window 0 5x 5100 by - 15165y51726 . Use the Intersection Feature to nd the break-even quantities The minimum break-even quantity is 12' peeks ofpeppers. The maximum break-even quantity is 43' peaks of peppers. b. Wn'te the prot function Pix) = R(x) C(x]. Use a graphing Q utililyto also graph y3 = Pix] elonI with yourother two graphs. ' ' Q Pix) = - x2 + 60x - m l3 c. For what values of x is the prot P(x)=0? Q The lower value of x is 12'. a The higher value x is 48'. iii d. How many peaks of peppers should be produced for revenue to be maximized? What is the value of the maximum revenue? Producing 39' packs of pickled peppers resul; in a maximum revenue 01 5 1521'. e. How many packs of peppers should be produced for prot to be maximized? What is the value of the maximum prot? Producing 30' peeks of pickled peppers results in a maximum prot of S 324' f. Explore the relationship between the graphs 01 R. C, and P. Which isi'are true? Select all that apply. A. The xintieroepts of the graph of Pix) occur at the values ofx for which Rx) and C(x) intersect. B. The distance between the parabola R(x) and the line C(x) is greatest at the value of): which makes the prot Pb!) maximum. c. Once Peter produces enoth peaks of pickled peppers torst breakeven, he will eventually aIain reach a point where he will have a negative prot {loss} ifhe keeps producing packs ofpickied peppers. This is because the Iraphs of C(x} and Rix] intersect twice