I need help on all three

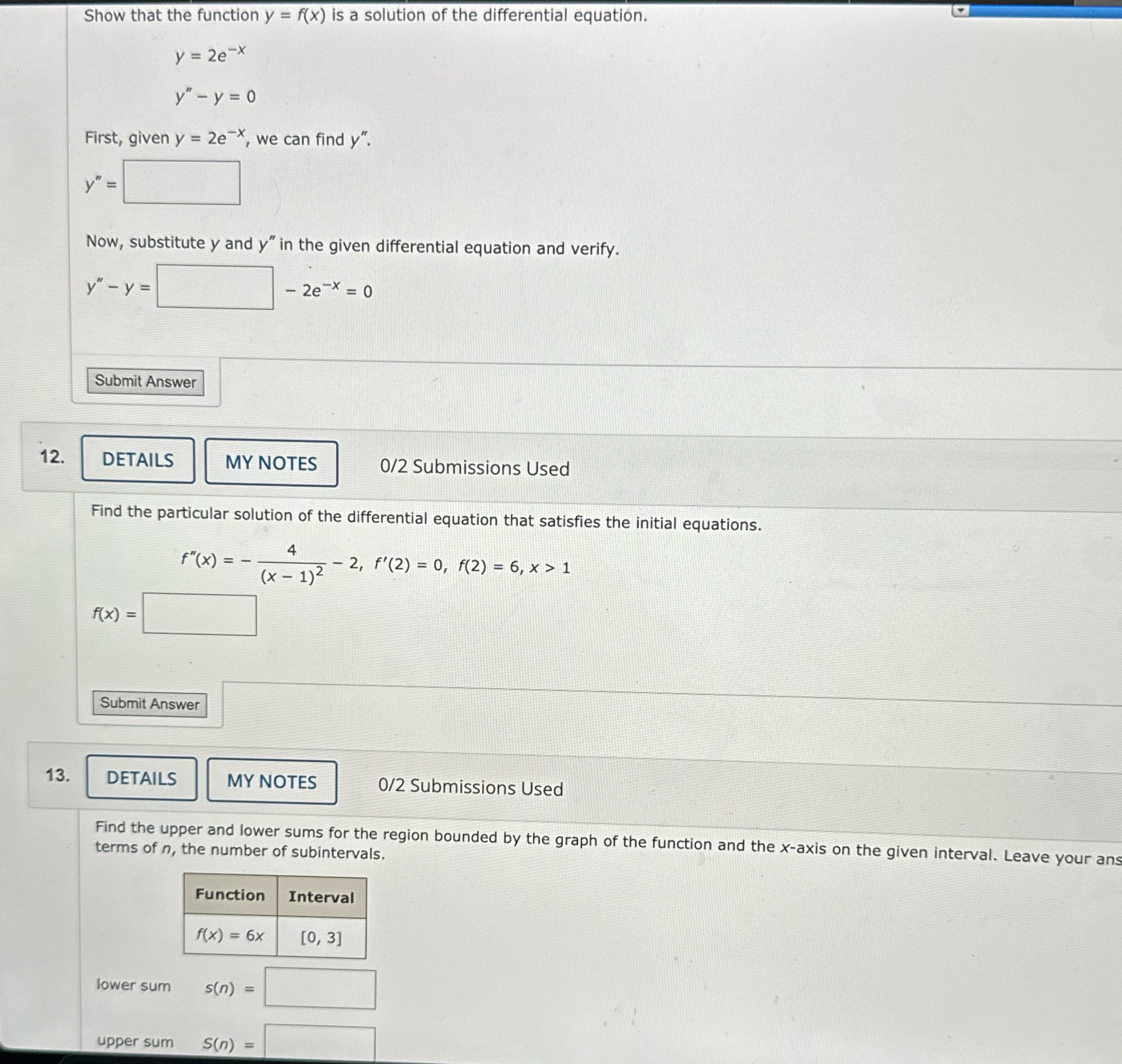
Show that the function y = f(x) is a solution of the differential equation. y = 2e-x y " - y = 0 First, given y = 2e *, we can find y". y " Now, substitute y and y" in the given differential equation and verify. y" - y = - 2e-X = 0 Submit Answer 12 DETAILS MY NOTES 0/2 Submissions Used Find the particular solution of the differential equation that satisfies the initial equations. f" (x) = (x - 1) 2 - 2, f' (2) = 0, f(2) = 6, x > 1 f ( x ) = Submit Answer 13 DETAILS MY NOTES 0/2 Submissions Used Find the upper and lower sums for the region bounded by the graph of the function and the x-axis on the given interval. Leave your an terms of n, the number of subintervals. Function Interval f(x) = 6x [0, 3] lower sum s ( n ) = upper sum S(n) =