I need help please with this question, by using manning's formula

Q1: Using the peak dry weather flow ( 2.5 MGD ) and following the requirements of the design the sewer main from the new development, n=0.013

Use the nomograph below to determine.

• What diameter pipe should be used if the slope is 1.5%?
• What slope is required to ensure at least the minimum allowable velocity (2 ft/s ) during peak dry weather flow?

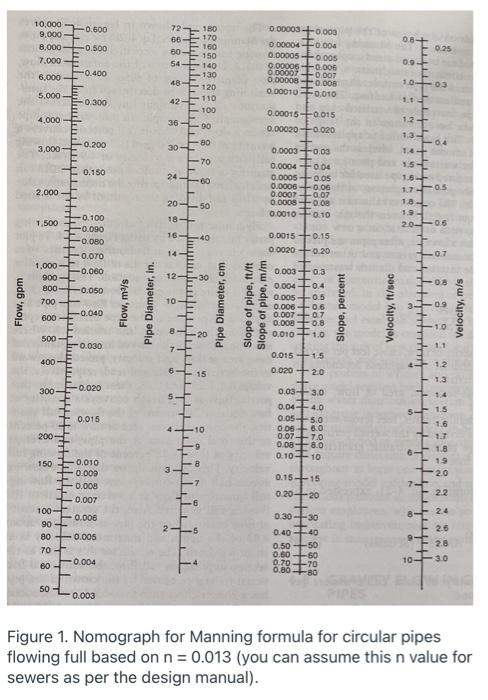
10,000 - 0.600 9.000 8,000 - 50.500 7,000 0.8-+ 0.25 72 7180 86-170 160 00- 150 54 140 130 48- 120 000003 +0.000 O 00004 0.004 0.00005 +0.005 0.00006 +0.00 0.00008 +0.000 popoz +0.001 0.00010 F0010 09- 6.000 -0.400 10-03 5,000 0.300 42-110 100 0.00015 +0.015 4,000 36 38 0.00020 +0.020 1.2 13 0.200 -80 3.000 04 30- -70 0.150 24 0.0003 +0.03 0.0004 +004 0.0005 -0.05 0.0006 -0.06 0.0007 +0.07 0.0008 0.0010 +0.10 1.5- 1.5 -60 2.000 170 2050 F 00 18 19- 1.500 18 20-06 16 -40 0.0015 +0.15 0.100 -0.090 -0.080 -0.070 -0.060 14 0.0020 +0.20 TTTTTTTT I! LLLL 07 12- -30 1,000 900 800 700 08 -0.050 Flow, 9pm Flow, m/s Pipe Diameter, in. 10 Pipe Diameter, cm ft/lt pipe, Slope of pipe, m/m Slope 0.003+03 0.004 -0.4 0.005 0.5 0.006 +0.6 0.007+0.7 0.008 +0.8 0.010 +1.0 09 Slope, percent Velocity, ft/sec -0.040 Velocity, m/s 600 LLLLLLL -10 20 500 0.030 7 1.1 0.015-1.5 400 4 1.2 6 15 0.020 +2.0 + 1.3 300+ 0.020 5 1.4 TTT 51.5 0.015 4 0.03 + 3.0 0.04 - 4.0 0.05-50 0.06 + 6.0 0.07 +7.0 0.08 +8.0 0.10-10 10 200 1.6 1.7 1.8 1 20 22 150 0.010 0.009 -0.008 0.007 100- 0.000 90 80 +0.005 70 60 0.004 824 Ti 0.15-15 0.20+20 + 0.30+30 0.4040 0.50 +50 0.60+60 0.70 +70 0.80 +80 2.6 9- 2.8 10-30 50 0.003 Figure 1. Nomograph for Manning formula for circular pipes flowing full based on n = 0.013 (you can assume this n value for sewers as per the design manual)