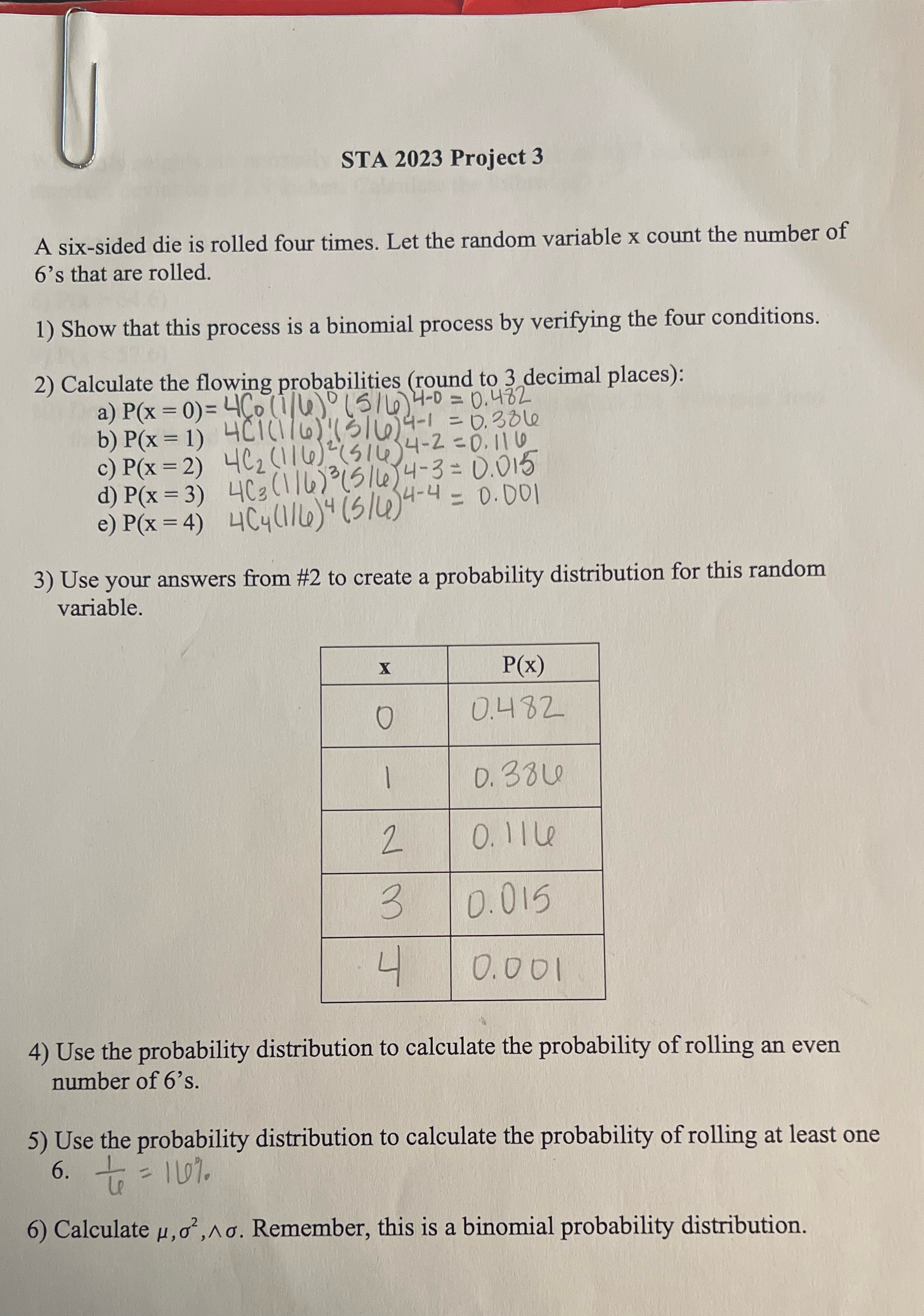
Question: I need help with #6 STA 2023 Project 3 A six-sided die is rolled four times. Let the random variable x count the number of
I need help with #6
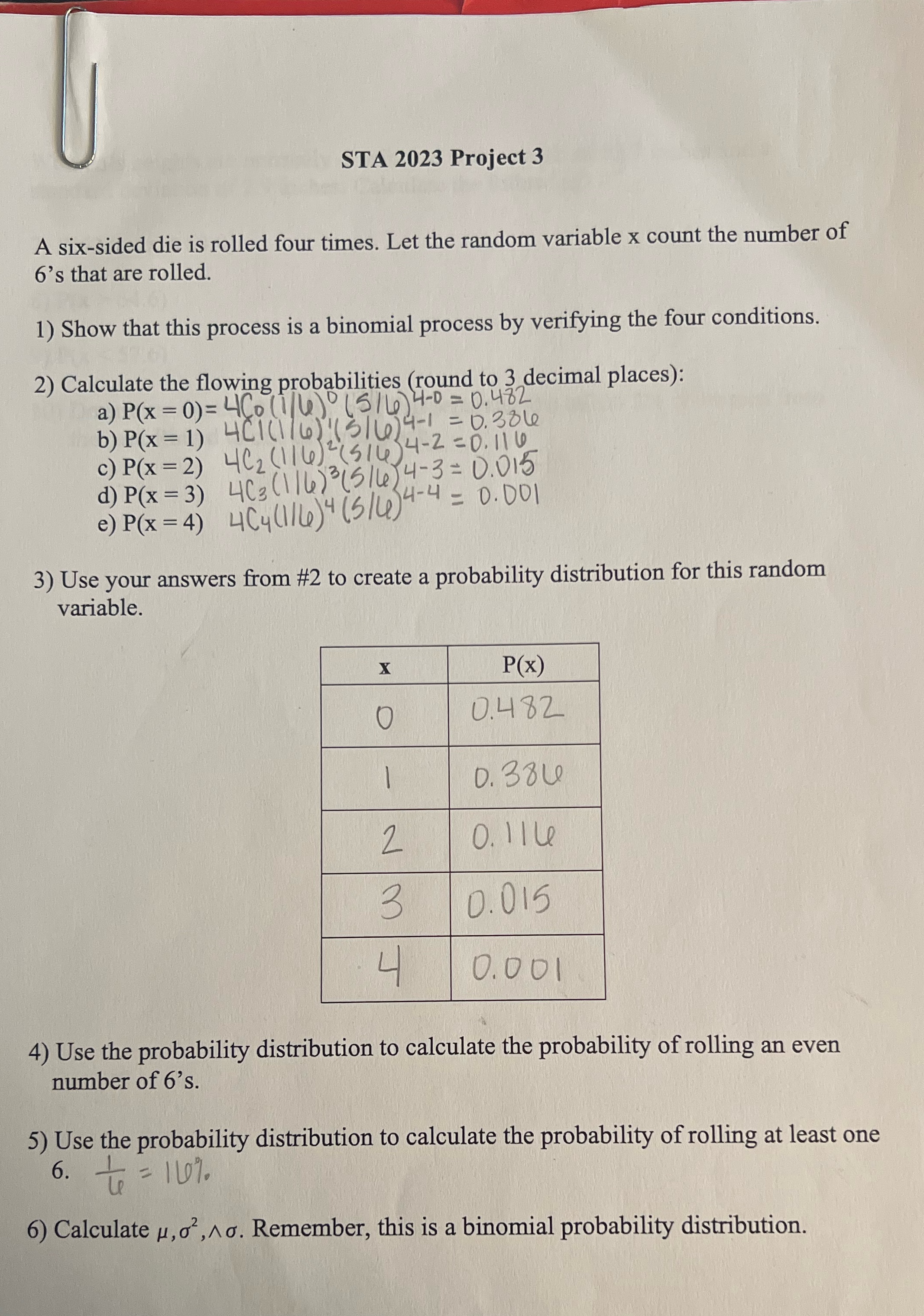
STA 2023 Project 3 A six-sided die is rolled four times. Let the random variable x count the number of 6's that are rolled. 1) Show that this process is a binomial process by verifying the four conditions. 2) Calculate the flowing probabilities (round to 3 decimal places): a) P(x = 0) = 4Co (1/ 4) (5 /4) 4-0 = 0. 482 14- 1 = 0.30 le b) P(x = 1) 4C1(1 /6); (510/ 4-2 = 0. 110 c) P(x = 2) 462 (114)=(510)-3= 0.010 d) P(x = 3) 403 (1/4) (21424-4 = 0.001 e) P(x = 4) 404(114)4 (5/4)4 3) Use your answers from #2 to create a probability distribution for this random variable. X P(X) O 0. 482 - D. 384 2 O. Ille 3 0. 015 L 0.001 4) Use the probability distribution to calculate the probability of rolling an even number of 6's. 5) Use the probability distribution to calculate the probability of rolling at least one 6. . = 169. 6) Calculate #,o', A. Remember, this is a binomial probability distribution
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


