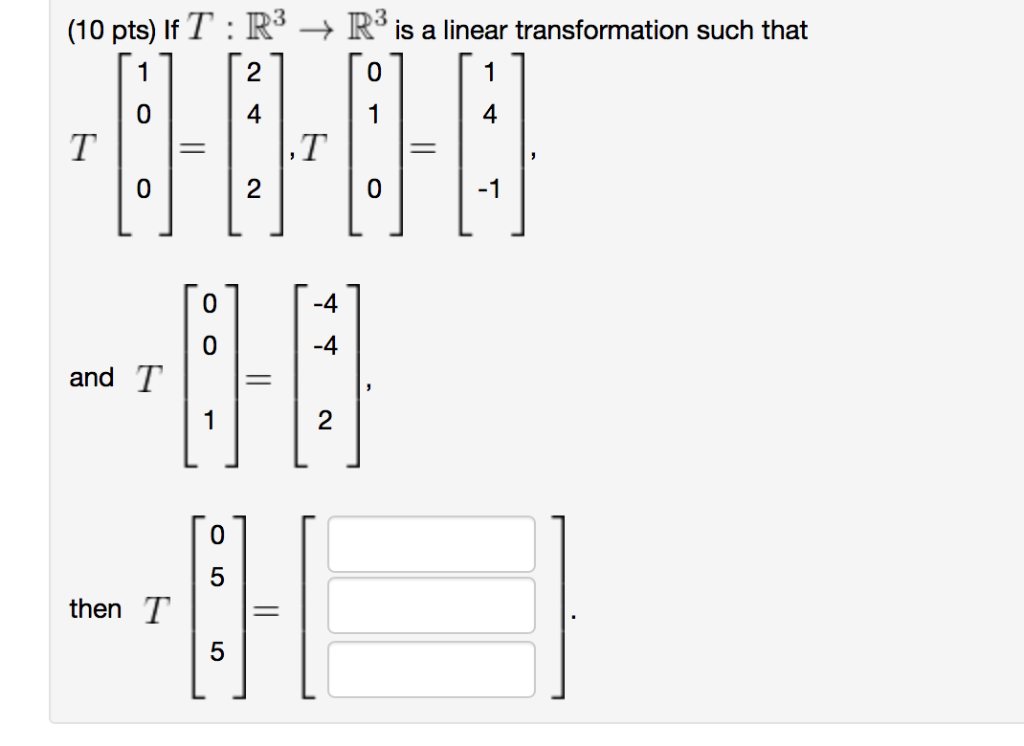
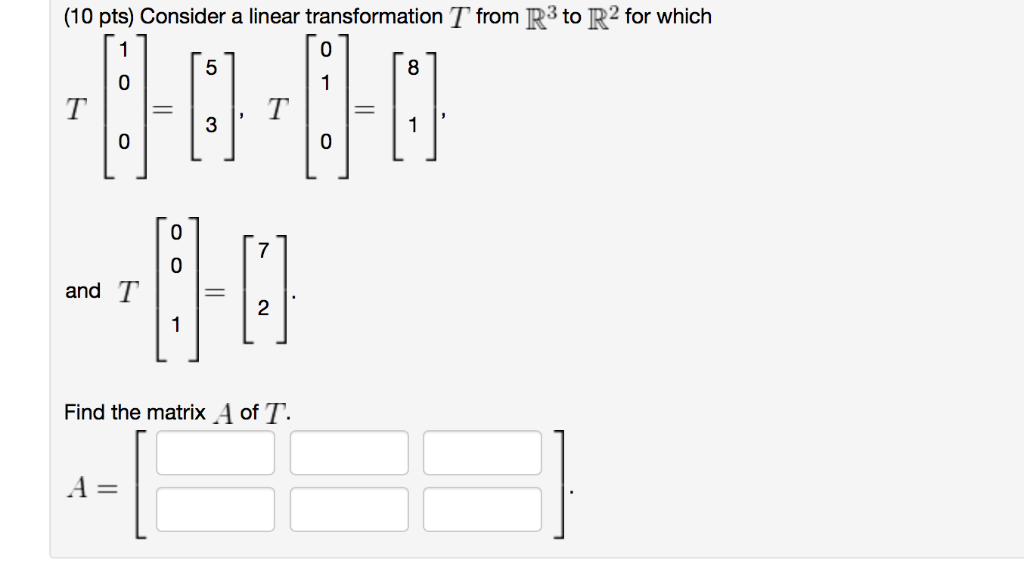
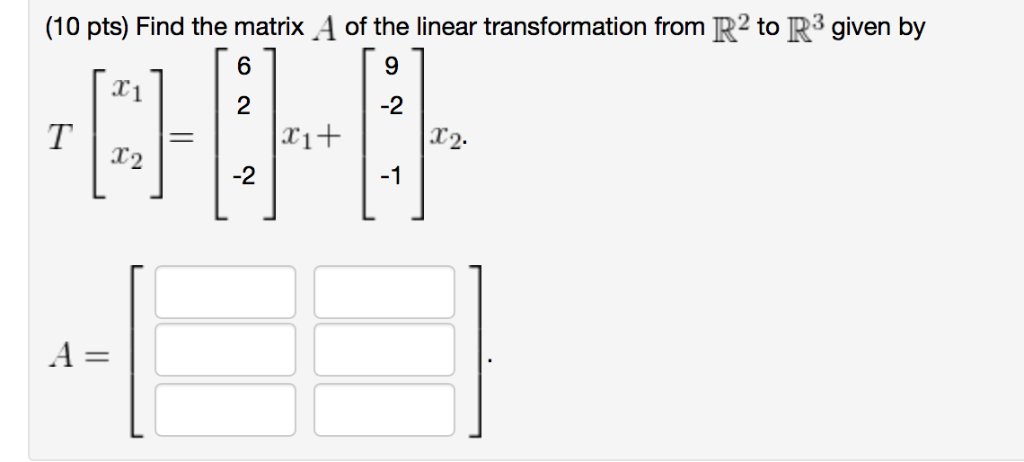
(10 pts) Which of the following transformations are linear? A. B. C. D. E. F. Y=-5x Y2=8x1 Y3=9x y/=0 Y2=X1X2 y=2 Y2=10 Y3=4 Y x + 7 Y2=X2 Y=0 Y2=10x2 Y=4x2 Y2=-9x3 Y3=-3x (10 pts) If T: R R is a linear transformation such that 2 4 1 -0-0-0-0 T = T = 2 and T 0 0 1 = -4 + 2 0 5 -HE then T 5 1 4 -1 (10 pts) If T: R R is a linear transformation such that 5 +C]-[-]-~-0-[] and T -2 T -9 then the standard matrix of T is A = (10 pts) Match each linear transformation with its matrix. 01 10 10 00 -10 01 20 02 01 [*] -10 1. 2. 3. 4. 5. 01 -10 -10 A 0-1 5. 6. A. Reflection in the y-axis B. Reflection in the origin C. Rotation through an angle of 90 in the clockwise direction D. Projection onto the x-axis E. Reflection in the line y = x F. Dilation by a factor of 2 (10 pts) Consider a linear transformation T from R to R2 for which 5 1 8000 T 3 T --0-0 and T 2 1 Find the matrix A of T. A = 1 (10 pts) Find the matrix A of the linear transformation from R2 to R given by 6 9 -2 = x+ -2 -1 T A = x1 X2 x2. (10 pts) -4 -4 -3 0 -1 2 A linear transformation T: R R is defined by T(x) = Ax. Find an, in R2 whose image under T is b. Let A = X2 and b = 24 9 -3 (10 pts) Find the matrix of the linear transformation from R2 to R2 that rotates any vector through an angle of 60 in the clockwise direction. [NOTE: if you answer use cos(...) and sin(...), webwork expects the arguments to be in RADIANS.] A = (10 pts) The dot product of two vectors in R is defined by a1 b a b a3 Let U = b3 9 6 -1 = ab + a2b2 + a3b3. Find the matrix of the linear transformation from R to R given by T(x) = = V.x. A = (10 pts) Let I be the line in R3 that consists of all scalar multiples of the vector 2 1 -2 Find the orthogonal projection of the vector 5 6 v= onto L. 1 projLv = (10 pts) Let I be the line in R3 that consists of all scalar multiples of the vector 6 ----- V= 3 in the line L. 3 -2 [] 2 Refl, (v) = = Find the reflection of the vector