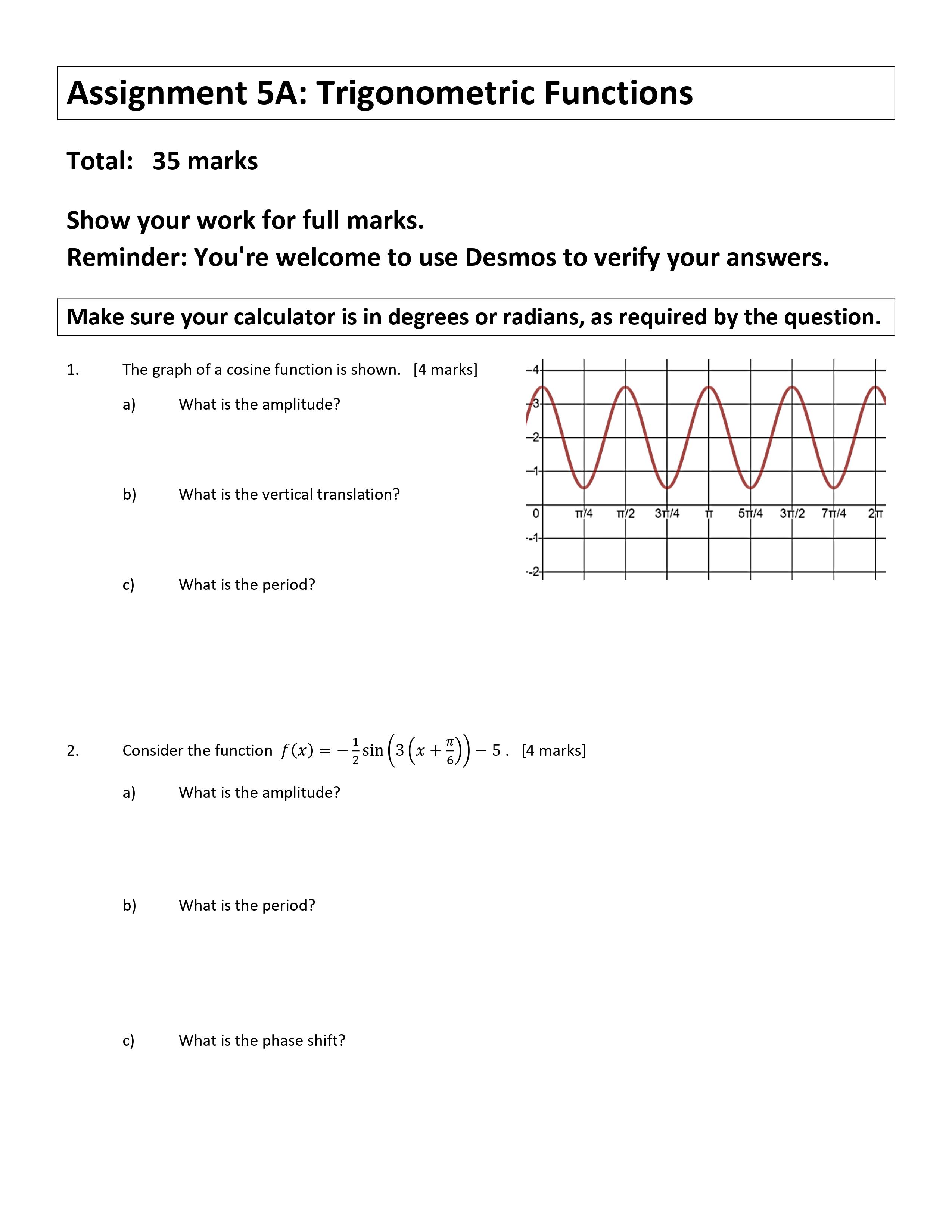
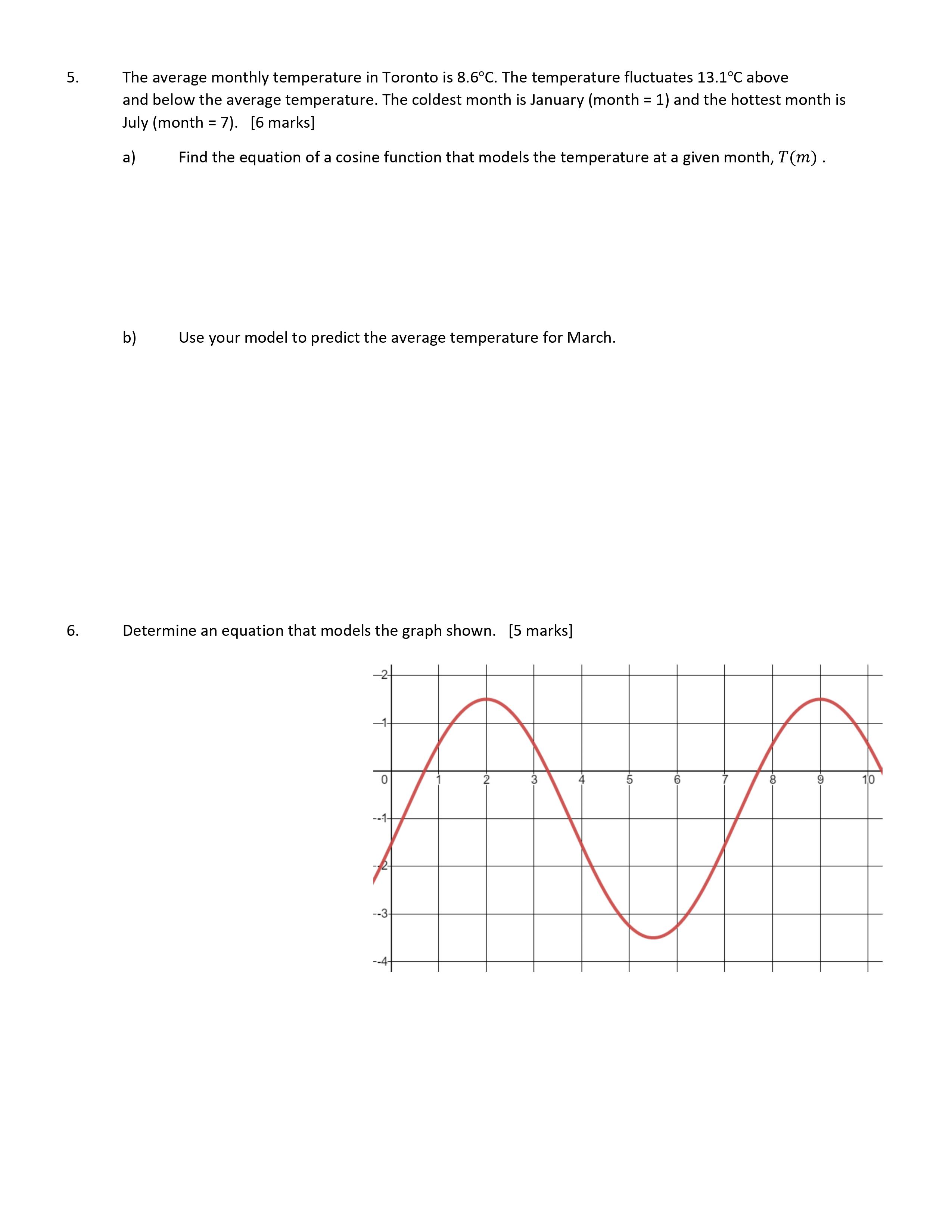
Question: I need help with my math homework Assignment 5A: Trigonometric Functions Total: 35 marks Show your work for full marks. Reminder: You're welcome to use
I need help with my math homework


Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


