Question: I need help with problem 5 5 Suppose f:RR is a Lebesgue measurable function. Prove that f(b)f(b) for almost every bR. 4A Hardy-Littlewood Maximal Function
I need help with problem 5 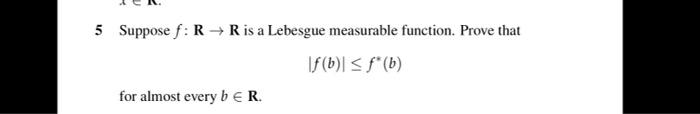




5 Suppose f:RR is a Lebesgue measurable function. Prove that f(b)f(b) for almost every bR. 4A Hardy-Littlewood Maximal Function Markov's Inequality The following result, called Markov's inequality, has a sweet, short proof. We will make good use of this result later in this chapter (see the proof of 4.10). Markov's inequality also leads to Chebysher's inequality (see Exercise 2 in this section). 4.1 Markov's inequality Suppose (X,S,) is a measure space and hL1(). Then ({xX:h(x)c})c1h1 for every c>0. Proof Suppose c>0. Then ({xX:h(x)c})=c1{xX:h(x)c}cduc1{xX:h(x)c}hdc1h1 as desired. St. Petersburg University along the Neva River in St. Petersburg. Russia. Andrey Markov (1856-1922) was a student and then a faculty member here. CC-BY.SA A. Savin 4.2 Definition 3 times a bounded nonempty open interval Suppose I is a bounded nonempty open interval of R. Then 3I denotes the open interval with the same center as I and three times the length of I. 4.3 Example 3 times an interval If I=(0,10), then 3+I=(10,20). The next result is a key tool in the proof of the Hardy-Littlewood maximal inequality (4.8). 4.4. Vitali Covering Lemma Suppose I1,,In is a list of bounded nonempty open intervals of R. Then there exists a disjoint sublist Ik1,,Ikm such that I1Im(3Ik1)(3Ikm). 4.5 Example Vitali Covering Lemma Suppose n=4 and I1=(0,10).I2=(9,15).I3=(14,22),I4=(21,31). Then 3I1=(10,20),3I2=(3,21),3I3=(6,30),3I4=(11,41). Thus I1I2I3I4(3I1)(3I4). In this example, I1,I4 is the only sublist of I1,I2,I3,I4 that produces the conclusion of the Vitali Covering Lemma. Prool of 4.4 Let k1 be such that Ik1=max{I1,,In}. Suppose k1,,kj have been chosen. Let kj+1 be such that Ikj+1 is as large as possible subject to the condition that Ik1,,Ikj+1 are disjoint. If there is no algorithm because at each choice of kj+1 such that Ik1,,Iki+1 are stage we select the largest remaining interval that is disjoint from the previously selected intervals. disjoint, then the procedure terminates. Because we start with a finite list, the procedure must eventually terminate after some number m of choices. Suppose j{1,,n}. To complete the proof, we must show that Ij(3Ik1)(3Ikm). If j{k1,,km}, then the inclusion above obviously holds. Thus assume that j/{k1,,km}. Because the process terminated without selecting j, the interval Ij is not disjoint from all of Ik1,,Ik10. Let Ik2 be the first interval on this list not disjoint from Ij; thus Ij is disjoint from Ik1,,IkL1. Because j was not chosen in step L, we conclude that IkLIj. Because IkLIj=, this last inequality implies (easy exercise) that Ij3=IkL, completing the proof. Hardy-Littlewood Maximal Inequality Now we come to a brilliant definition that tums out to be extraordinarily useful. 4.6 Definition Hardy-Littlewood maximal function; h Suppose h:RR is a Lebesgue measurable function. Then the HardyLittlewood maximal function of h is the function h:R[0,] defined by h(b)=supt>02t1btb+th. In other words, h(b) is the supremum over all bounded intervals centered at b of the average of h on those intervals. 4.7 Example Hardy-Linlewood maximal function of 0,1} As usual, let [0,1] denote the characteristic function of the interval [0,1]. Then ([0,1])(b)=2(1b)112b1ifb0if0c} is an open subset of R, as you are asked to prove in Exercise 9 in this section. Thus h is a Borel measurable function. Suppose hL1(R) and c>0. Markov's inequality (4.1) estimates the size of the set on which h is larger than c. Our next result estimates the size of the set on which h is larger than c. The Hardy-Littlewood maximal inequality proved in the next result is a key ingredient in the proof of the Lebesgue Differentiation Theorem (4.10). Note that this next result is considerably deeper than Markov's inequality. Measire, Integration \& Real Analysis, by Sheldon Axler 4.8 Hardy-Littlewood maximal inequality Suppose hL1(R). Then {bR:h(b)>c}c3h1 for every c>0. Prool Suppose F is a closed bounded subset of {bR:h(b)>c}. We will show that Fc3h, which implies our desired result [see Exercise 24(a) in Section 2D]. For each bF, there exists tb>0 such that 4.9 2tb1btbb+tbh>c. Clearly FbF(btb,b+tb). The Heine-Borel Theorem (2.12) tells us that this open cover of a closed bounded set has a finite subcover. In other words, there exist b1,,bnF such that F(b1tb1,b1+tb1)(bntbn,bn+tbn). To make the notation cleaner, relabel the open intervals above as I1,I4In. Now apply the Vitali Covering Lemma (4.4) to the list I1,.,IB. producing a disjoint sublist Ik1,,Ikie such that I1In(3Ik1)(3Ikm). Thus FI1In(3Ik1)(3Ikm)3Ik1++3Ikm=3(Ik1++Ikm)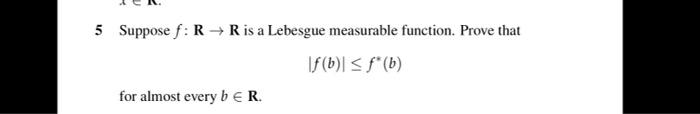




Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


