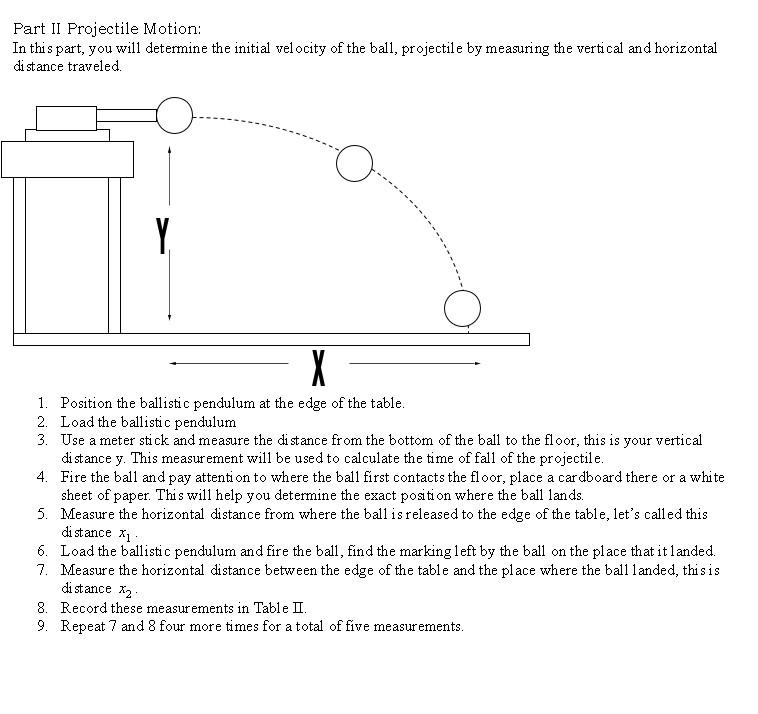
The Ballistic pendulum experiment combines two conservation laws; conservation of linear momentum and conservation of energy. If two objects collide and the only force present during the collision is the interaction between them, we could say that the total momentum of the system is conserved. Knowing that linear momentum is defined as mass in motion and calculated as: p=m. Then, we could write the Law as: Lab "The Ballistic Pendulum." (+) before = ( +P) after For the case of the ballistic pendulum object 1 is the ball and object 2 the cage of the pendulum. Since the pendulum is not moving before the collision then its initial momentum is zero. After collision the ball and the cage travel together, they have the same velocity. Then, we could write: mVox - (m + M)V where: equation 1 mis the mass of the ball, M is the mass of the Pendulum, Vis the initial velocity of the ball and V is the velocity after ball - pendulum after collision equation 2 Solving for the initial velocity of the ball: V = The Conservation of Energy states that the total mechanical energy of a system states constant. Which means that if the Kinetic energy of the system decreases the potential energy increases by the same amount. We could write: TE TE or AKE = AGPE Since in this case the mechanical energy is comprised of Kinetic and Gravitational potential energies and knowing that: m KE=m and GPE = mgy In our case, the pendulum stops at the final position y, Then we find that: w+M7 772 (m+M) V = (m+ M) g(-) equation 3 From this we find that the velocity of the ball-pendulum system V=2g(2-) equation 4 Before Collision M V Y2 After Collision Ballistic Pendulum of mass M before and after collision with ball of mass m. PROCEDURES: Part I Ballistic Pendulum WARNING Ensure the trajectory is clear before cocking the spring and while firing. Safety glasses are available upon request 1. Use a scale to measure the mass of the ball: m = 2. Slide the projectile ball (which has a hole in it) onto the rod of the spring gun. 2. When the ball has been placed on the rod, cock the gun by pushing against the ball until the latch catches. Be very careful not to get your hand caught in the spring gun mechanism!!! 3. Fire the gun several times to see how it operates. Ensure the ball lands in the pendulum arm. If you cannot get the arm to catch properly, ask for help. There are several common problems: The height of the pendulum arm may be off. The opening of the pendulum arm may be at an angle The pendulum arm opening may be loose (which will rotate when the ball hits it, instead of catching it). The pivots at the top of the pendulum arm may be too tight or too loose. 4. A sharp curved point on the side of the pendulum (or on some models a dot) marks the center of mass of the pendulum-ball system. Let the pendulum bob hang vertically and measure the distance , of the point marking the center of mass above the base of the gun. Record the value of y= = cm 5. Place the ball on the rod, push against the call to cock the gun, and fire the ball into the stationary pendulum while it hangs freely at rest. The pendulum will catch the ball, swing up, and then lodge in the notched track. 6. Record the vertical distance from the bottom of the base to the center of mass of the ball-pendulum system in Data Table I. 7. Repeat step 6 four more times for a total of five measurements. 8. Loosen the screws holding the pendulum in its support and remove the pendulum. Use a scale and measure the mass of the pendulum: M = Part II Projectile Motion: In this part, you will determine the initial velocity of the ball, projectile by measuring the vertical and horizontal distance traveled. Y O X 1. Position the ballistic pendulum at the edge of the table. 2. Load the ballistic pendulum 3. Use a meter stick and measure the distance from the bottom of the ball to the floor, this is your vertical distance y. This measurement will be used to calculate the time of fall of the projectile. 4. Fire the ball and pay attention to where the ball first contacts the floor, place a cardboard there or a white sheet of paper. This will help you determine the exact position where the ball lands. 5. Measure the horizontal distance from where the ball is released to the edge of the table, let's called this distance X 6. Load the ballistic pendulum and fire the ball, find the marking left by the ball on the place that it landed. 7. Measure the horizontal distance between the edge of the table and the place where the ball landed, this is distance . 8. Record these measurements in Table II. 9. Repeat 7 and 8 four more times for a total of five measurements. 10. Check that the Law of Conservation of Momentum is held in this experiment: Calculate the change in momentum of the Ball: Ap = Pf-Pi = m(V - Vox)=69(114.59-521.47)=-28074.72 Calculate the change in momentum of the Pendulum: AP = Pf-P = M(V - 0)=245(114.59-0)=28074.55 Calculate the Total change in momentum of the system, explain its meaning: Aps = Ap+ AP =-28074.72+28074.55=-0.17 system 11. What is the meaning of this result? 12. Check that the Law of Conservation of Energy holds in this experiment: