I need help with question 4 please.

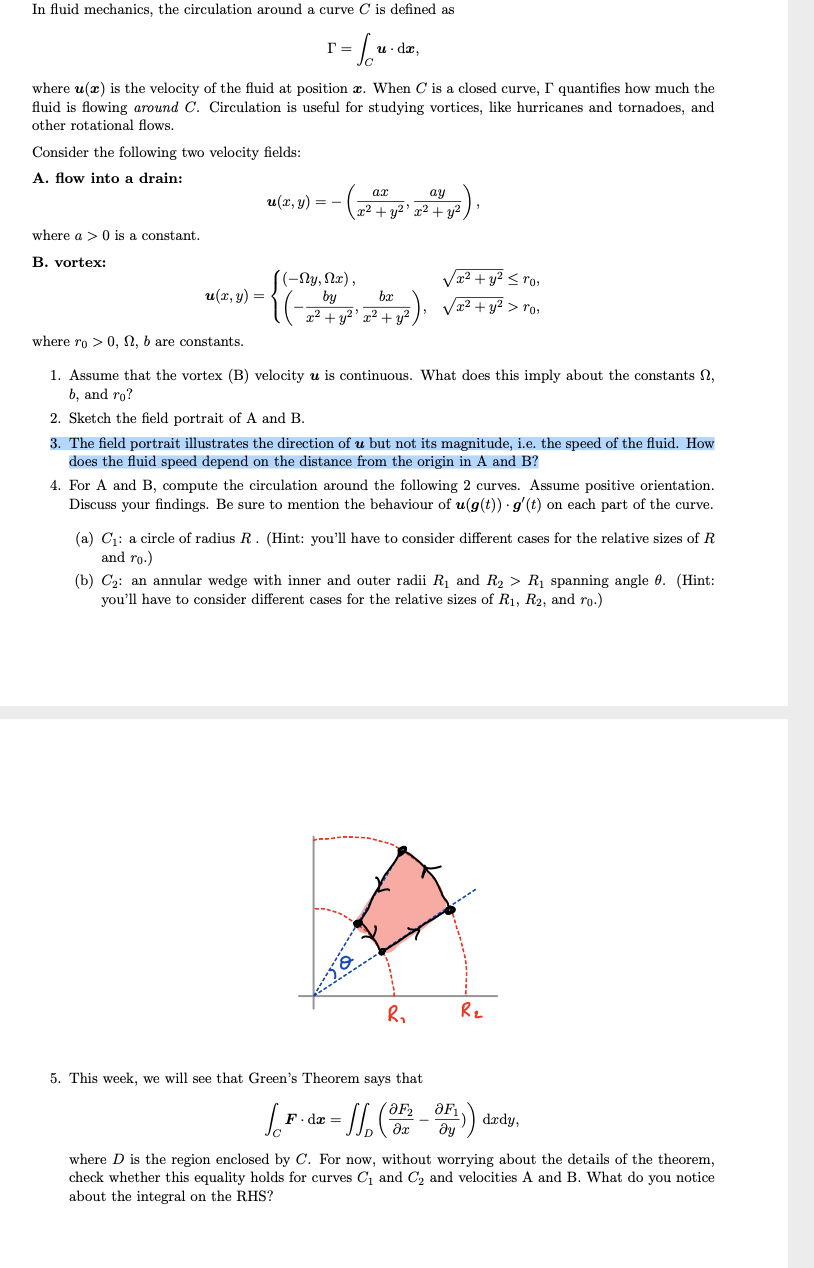
In fluid mechanics, the circulation around a curve C is defined as T = u. dx, where u(x) is the velocity of the fluid at position x. When C is a closed curve, I' quantifies how much the fluid is flowing around C. Circulation is useful for studying vortices, like hurricanes and tornadoes, and other rotational flows. Consider the following two velocity fields: A. flow into a drain: u(x, y) = - ax ay where a > 0 is a constant. B. vortex: (-ny, n1) , u(x,v)= Va2+y'sro, by bx Vaz +y' > ro, where ro > 0, 0, b are constants. 1. Assume that the vortex (B) velocity u is continuous. What does this imply about the constants , b, and ro? 2. Sketch the field portrait of A and B. 3. The field portrait illustrates the direction of u but not its magnitude, i.e. the speed of the fluid. How does the fluid speed depend on the distance from the origin in A and B? 4. For A and B, compute the circulation around the following 2 curves. Assume positive orientation. Discuss your findings. Be sure to mention the behaviour of u(g(t)) . g'(t) on each part of the curve. (a) Ci: a circle of radius R . (Hint: you'll have to consider different cases for the relative sizes of R and ro.) (b) C2: an annular wedge with inner and outer radii R, and R2 > R, spanning angle 0. (Hint: you'll have to consider different cases for the relative sizes of R1, R2, and ro.) Re 5. This week, we will see that Green's Theorem says that aFi) ) dady , where D is the region enclosed by C. For now, without worrying about the details of the theorem, check whether this equality holds for curves C, and C2 and velocities A and B. What do you notice about the integral on the RHS