I need help with this problem, and it's looking difficult

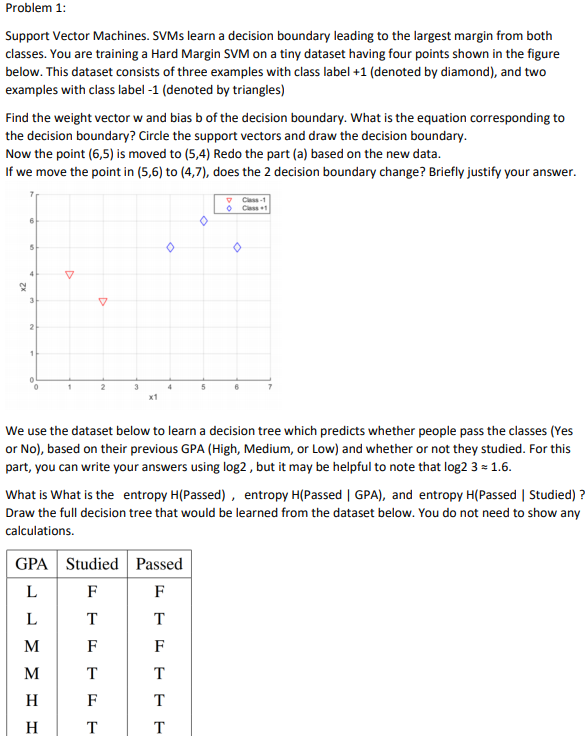
Problem 1: Support Vector Machines. SVMs learn a decision boundary leading to the largest margin from both classes. You are training a Hard Margin SVM on a tiny dataset having four points shown in the figure below. This dataset consists of three examples with class label +1 (denoted by diamond), and two examples with class label -1 (denoted by triangles) Find the weight vector w and bias b of the decision boundary. What is the equation corresponding to the decision boundary? Circle the support vectors and draw the decision boundary. Now the point (6,5) is moved to (5,4) Redo the part (a) based on the new data. If we move the point in (5,6) to (4,7), does the 2 decision boundary change? Briefly justify your answer. Class -1 O O V V We use the dataset below to learn a decision tree which predicts whether people pass the classes (Yes or No), based on their previous GPA (High, Medium, or Low) and whether or not they studied. For this part, you can write your answers using log2 , but it may be helpful to note that log2 3 = 1.6. What is What is the entropy H(Passed) , entropy H(Passed | GPA), and entropy H(Passed | Studied) ? Draw the full decision tree that would be learned from the dataset below. You do not need to show any calculations. GPA Studied Passed F F L T T M M T HAAT H F H T