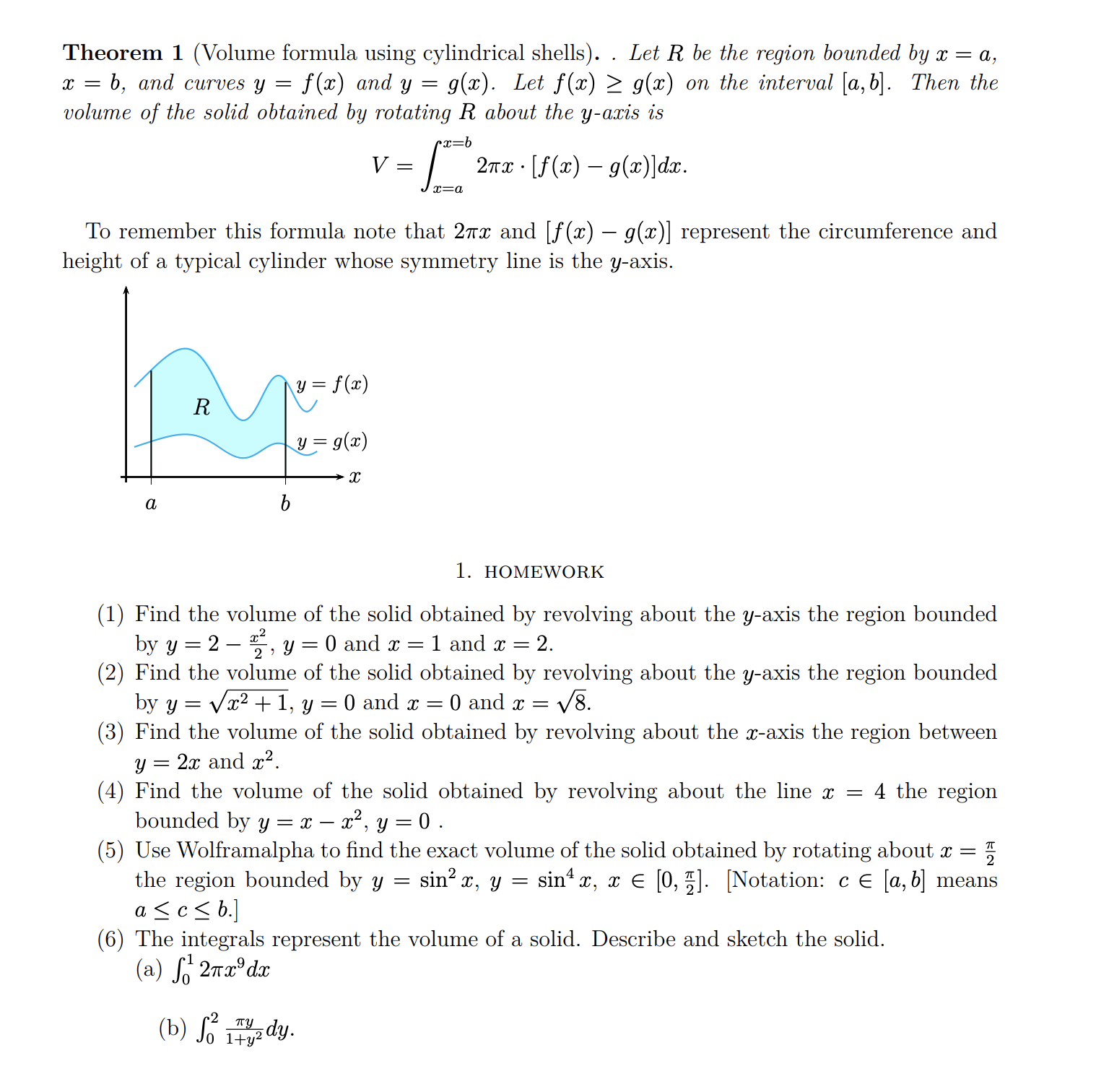
Question: I need it asap Theorem 1 (Volume formula using cylindrical shells). . Let R be the region bounded by :1: = a, x = b,
I need it asap
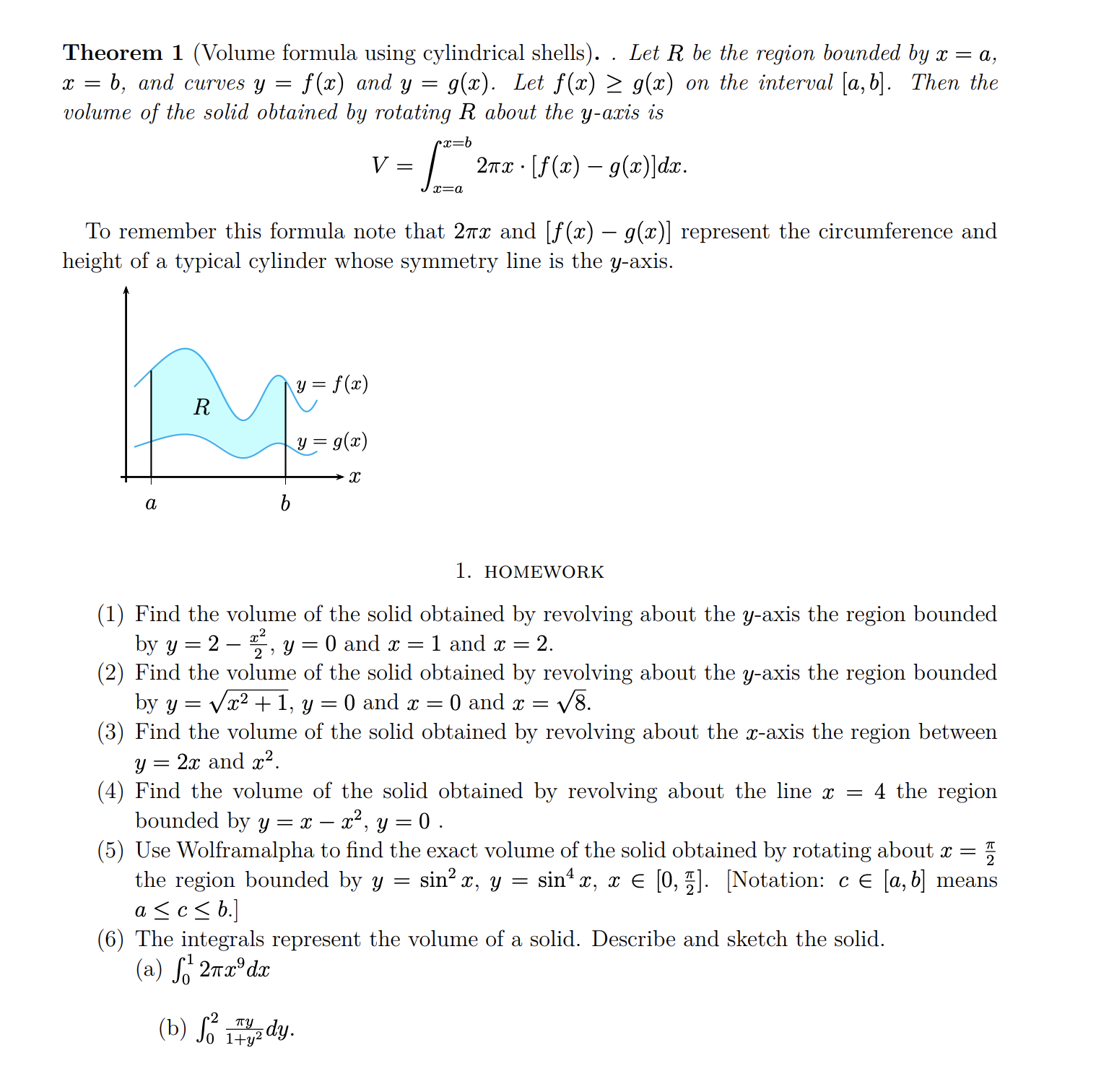
Theorem 1 (Volume formula using cylindrical shells). . Let R be the region bounded by :1: = a, x = b, and curves y = at) and y = 9(1). Let f(ac) 2 9(30) on the interval [a, b]. Then the volume of the solid obtained by rotating R about the y-oztis is V = [Rb 21m: - [f(a:) g(m)]dm. 13:0. To remember this formula note that 21m: and [f (:0) 9(3)] represent the circumference and height of a typical cylinder Whose symmetry line is the yaxis. l. HOMEWORK (1) Find the volume of the solid obtained by revolving about the yaxis the region bounded byy=2%2,y=0andm=1 andm=2. (2) Find the volume of the solid obtained by revolving about the yaxis the region bounded byy=\\/x2+1,y=0andm=0andx=x/. (3) Find the volume of the solid obtained by revolving about the maxis the region between 3; = 233 and 3:2. (4) Find the volume of the solid obtained by revolving about the line 3: = 4 the region bounded byy=5cm2, y=0. (5) Use Wolframalpha to nd the exact volume of the solid obtained by rotating about :6 = g the region bounded by y = sin2 3:, y = sin4 3:, :1: E [0% . [Notation: c 6 [a,b] means a S c S b.) (6) The integrals represent the volume of a solid. Describe and sketch the solid. (a) )3 21rm9dzc (b) 5 essay
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


