I need some help with last three questions. Previous relevant questions provided for context.

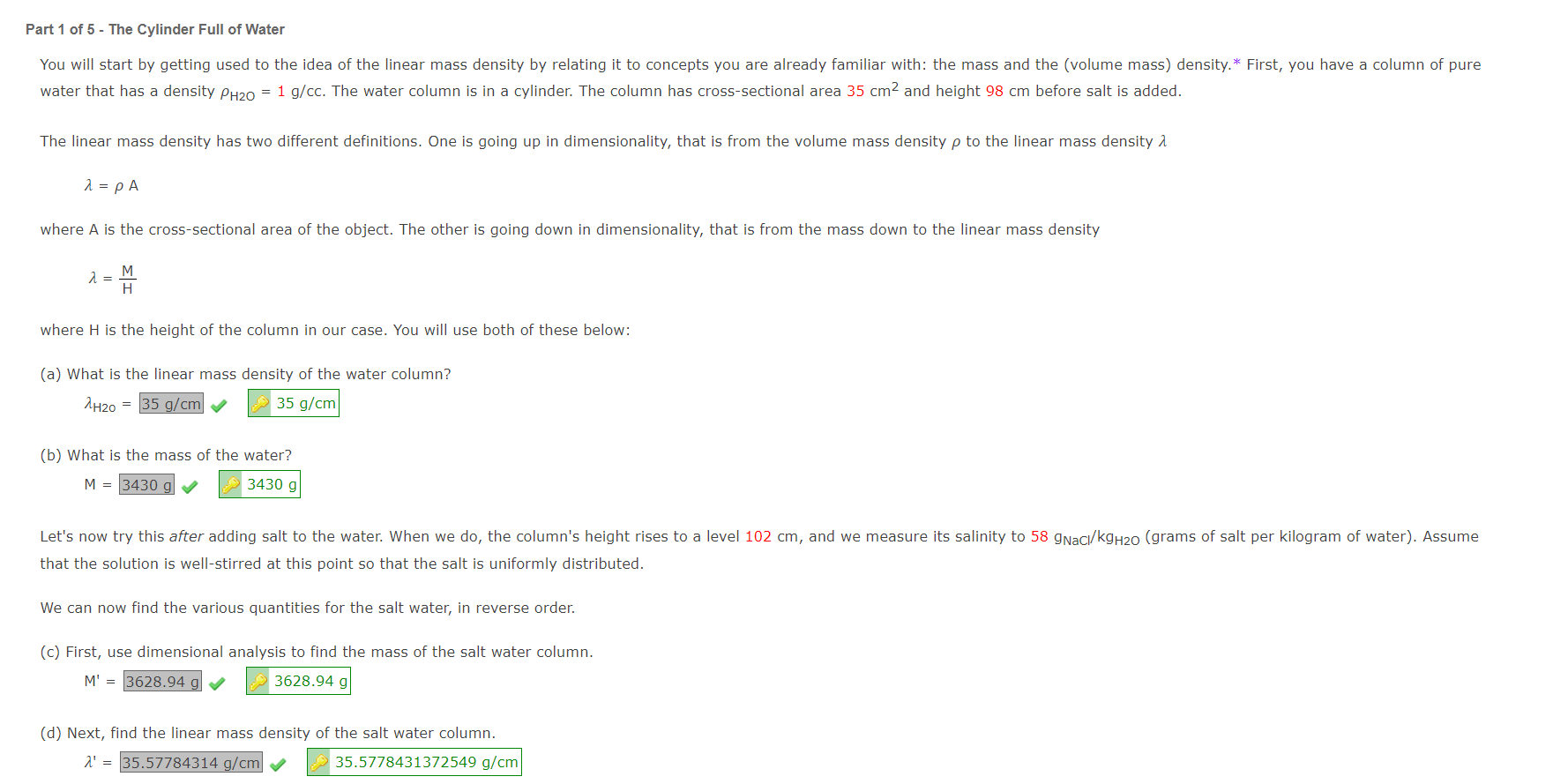
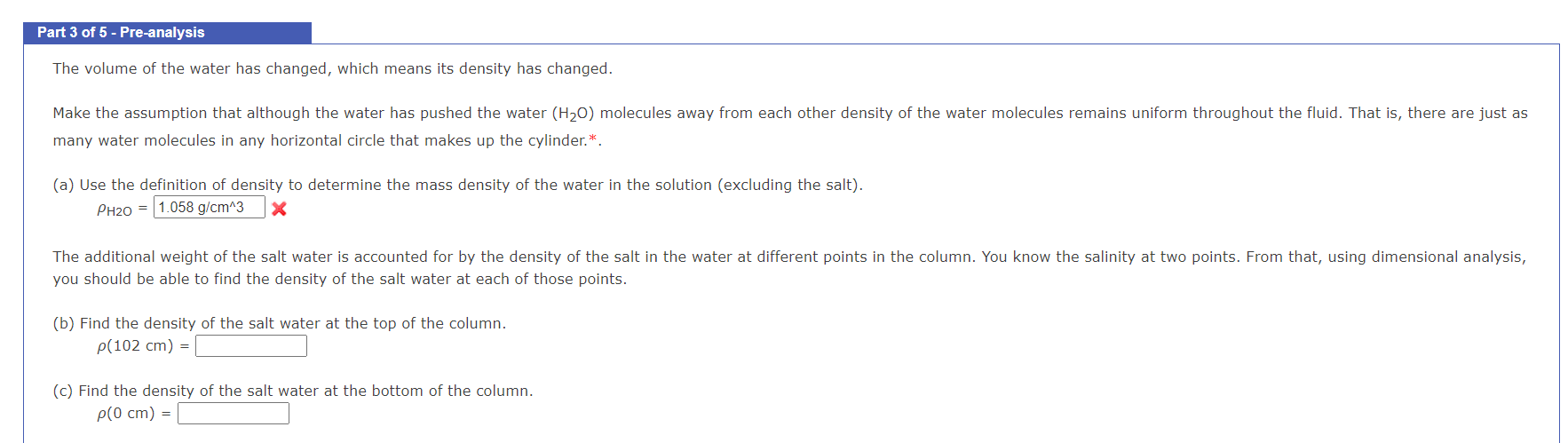
In this application, you will find the mass of a salt water column that has a varying salinity. Salt water gets heavier with a greater salinity, but it also increases the volume of the fluid when it's done. When the fluid is uniform, like in pure, distilled water, the mass of the water column can be found using the simplest definition, but when there is a gradient* in the density, which will happen if there is a gradient in the salinity, then the mass needs to be found through an integral formulation M=0H(z)dz with the mass of the fluid M being the sum over the masses of each of the infinitesimal circles dz that the cylinder is built up of. This is "technically zero," except when you sum up an infinite number of them with the integral. The function (z) is called the "linear mass density" of the fluid, it is way we characterize the 2D circle at a particular height z above the bottom of the cylinder. This allows us to say that the lower circles will be heavier than the highe Part 1 of 5 The Cylinder Full of Water water that has a density H2O=1g/cc. The water column is in a cylinder. The column has cross-sectional area 35cm2 and height 98cm before salt is added. The linear mass density has two different definitions. One is going up in dimensionality, that is from the volume mass density to the linear mass density =A where A is the cross-sectional area of the object. The other is going down in dimensionality, that is from the mass down to the linear mass density =HM where H is the height of the column in our case. You will use both of these below: (a) What is the linear mass density of the water column? H2O= (b) What is the mass of the water? M=3430g that the solution is well-stirred at this point so that the salt is uniformly distributed. We can now find the various quantities for the salt water, in reverse order. (c) First, use dimensional analysis to find the mass of the salt water column. M=3628.94g (d) Next, find the linear mass density of the salt water column. = (e) Finally, find the volume mass density. = The volume of the water has changed, which means its density has changed. many water molecules in any horizontal circle that makes up the cylinder.*. (a) Use the definition of density to determine the mass density of the water in the solution (excluding the salt). H2O=1.058g/cm3 you should be able to find the density of the salt water at each of those points. (b) Find the density of the salt water at the top of the column. (102cm)= (c) Find the density of the salt water at the bottom of the column. (0cm)=