I need some help with this problem.

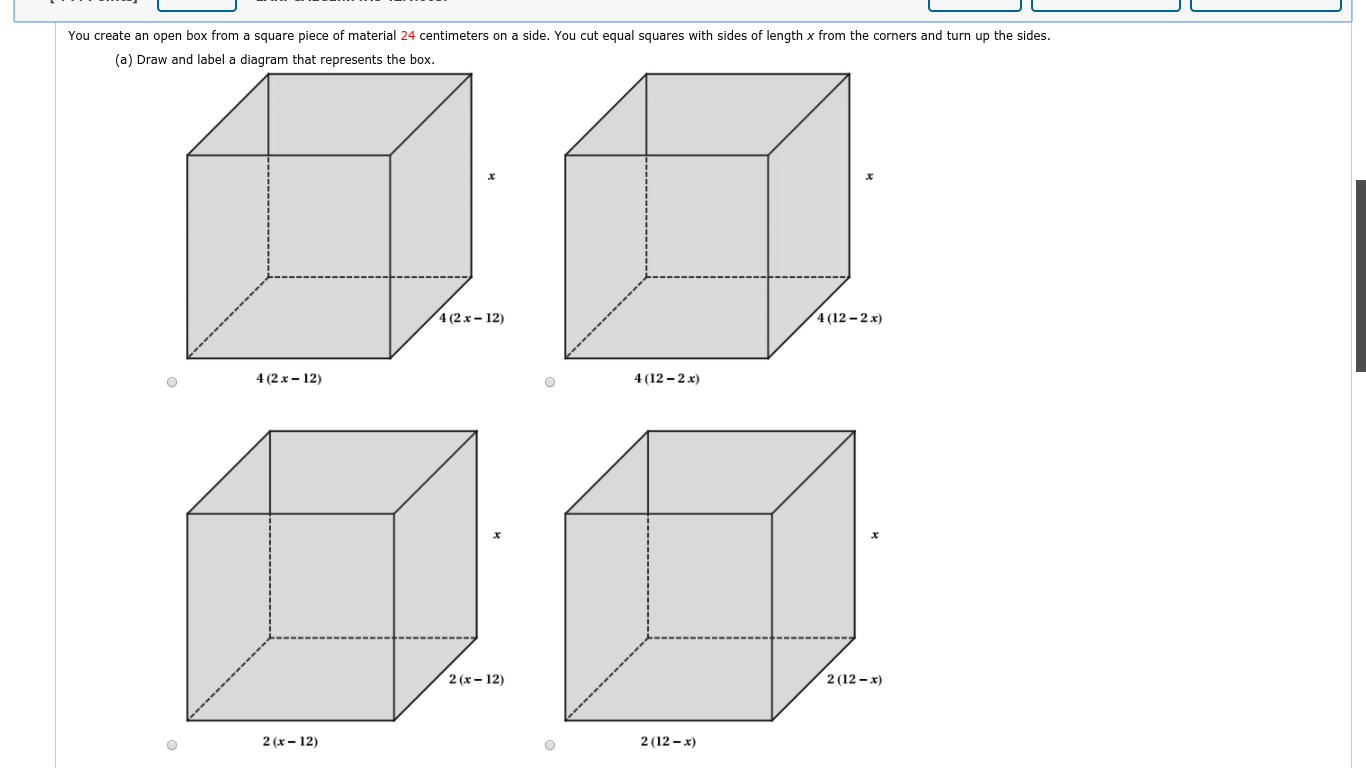
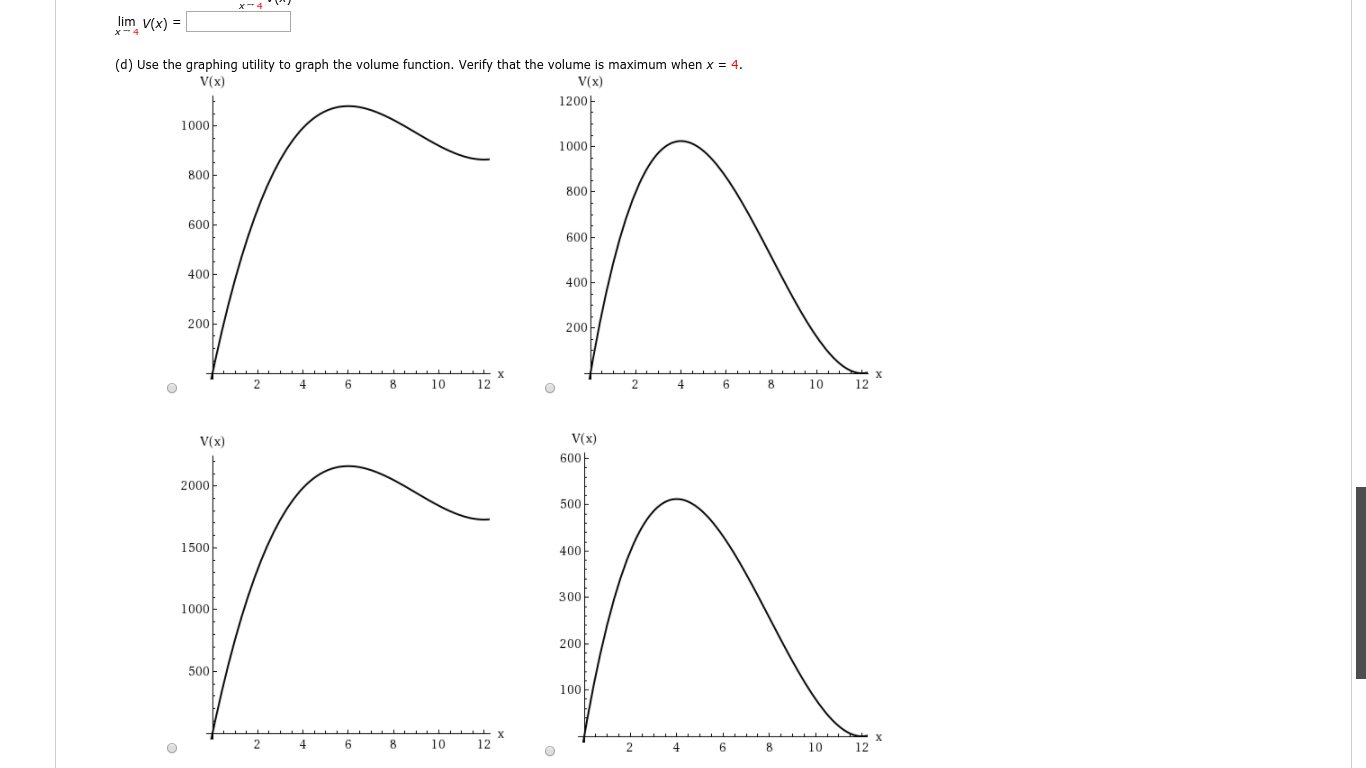
You create an open box from a square piece of material 24 centimeters on a side. You cut equal squares with sides of length x from the corners and turn up the sides. (a) Draw and label a diagram that represents the box. 4 (2 x - 12) 4 (12-2x) O 4 (2 x - 12) O 4 (12 -2x) 2 (x - 12) 2 (12-x) O 2 (x - 12) 2 (12-x)2 (x - 12) 2 (12-x) 2 (x - 12) O 2 (12-x) (b) Write a function V(x) that represents the volume of the box. V (x) = (c) The box has a maximum volume when x = 4. Use a graphing utility to complete the table and observe the behavior of the function as x approaches 4. (Round your answers to one decimal place.) V(x ) 3 3.5 3.9 4 4.1 4.5 5 Use the table to find lim V(x)- lim V(x) =lim V(x) = x - (d) Use the graphing utility to graph the volume function. Verify that the volume is maximum when x = 4. V(x) V(x) 1200 1000 1000- 800- 800 600 600 400 400 200 200 O 2 4 6 8 10 12 O 2 4 6 8 10 12 X V(x) V(x) 600 2000 500 1500 400 1000 300 200 500- 100 O 2 4 6 8 10 12 O 2 4 6 8 10 12 X