I need this exercise to be implemented in MATLAB. (Not Simulink)

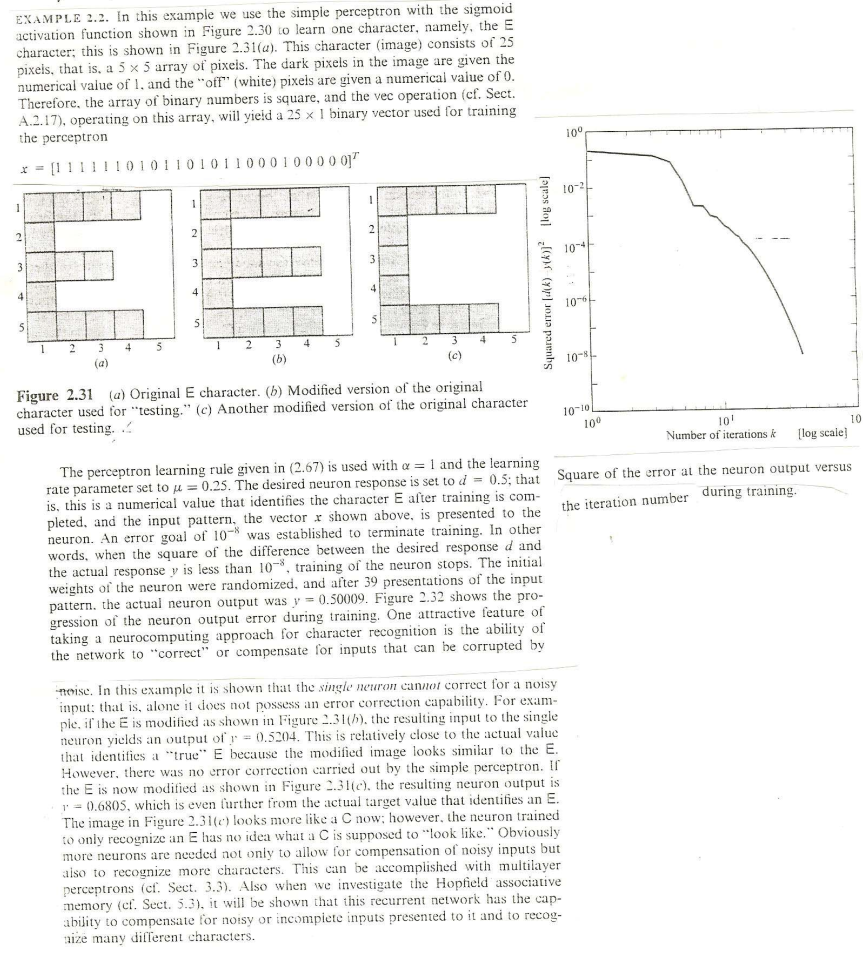
EXAMPLE 2.2. In this example we use the simple perceptron with the sigmoid activation function shown in Figure 2.30 to learn one character, namely, the E character; this is shown in Figure 2.31(a). This character (image) consists of 25 pixels, that is, a 5 x 5 array of pixels. The dark pixels in the image are given the numerical value of l. and the "off" (white) pixels are given a numerical value of 0. Therefore, the array of binary numbers is square, and the vec operation (cf. Sect. A.2.17), operating on this array, will yield a 25 x 1 binary vector used for training the perceptron [1111110101101011000100000" 100 10-2 1 1 2 2 N 10- 3 3 Squared error () ) flog scale] 4 4 4 106 s 5 5 5 4 5 3 4 1 2 4 5 5 2 3 (5) 3 (c) 10-8 10-10 100 Figure 2.31 (a) Original E character. (b) Modified version of the original character used for testing." (c) Another modified version of the original character used for testing. 10' 10 Number of iterations k [log scale) The perceptron learning rule given in (2.67) is used with a = 1 and the learning rate parameter set to u = 0.25. The desired neuron response is set to d = 0.5; that Square of the error at the neuron output versus is, this is a numerical value that identifies the character E after training is com- pleted, and the input pattern, the vector r shown above, is presented to the the iteration number during training. neuron. An error goal of 10- was established to terminate training. In other words, when the square of the difference between the desired response d and the actual response y is less than 10-, training of the neuron stops. The initial weights of the neuron were randomized, and after 39 presentations of the input pattern, the actual neuron output was y = 0.50009. Figure 2.32 shows the pro- gression of the neuron output error during training. One attractive feature of taking a neurocomputing approach for character recognition is the ability of the network to "correct" or compensate for inputs that can be corrupted by noise. In this example it is shown that the single neuron cannot correct for a noisy input: that is, alone it does not possess an error correction capability. For exam- ple, if the E is modified as shown in Figure 2.31(h), the resulting input to the single neuron yields an output of r = 0.5204. This is relatively close to the actual value that identifies a "true" E because the modified image looks similar to the E. However, there was no error correction carried out by the simple perceptron. Il the E is now modified as shown in Figure 2.31(c), the resulting neuron output is 1 = 0.6805, which is even further from the actual target value that identifies an E. The image in Figure 2.31(c) looks more like a C now: however, the neuron trained to only recognize an E has no idea what a C is supposed to "look like." Obviously more neurons are needed not only to allow for compensation of noisy inputs but also to recognize more characters. This can be accomplished with multilayer perceptrons (cf. Sect. 3.3). Also when we investigate the Hopfield associative memory (el. Sect. 5.3), it will be shown that this recurrent network has the cap- ability to compensate for noisy or incomplete inputs presented to it and to recog. size many different characters. EXAMPLE 2.2. In this example we use the simple perceptron with the sigmoid activation function shown in Figure 2.30 to learn one character, namely, the E character; this is shown in Figure 2.31(a). This character (image) consists of 25 pixels, that is, a 5 x 5 array of pixels. The dark pixels in the image are given the numerical value of l. and the "off" (white) pixels are given a numerical value of 0. Therefore, the array of binary numbers is square, and the vec operation (cf. Sect. A.2.17), operating on this array, will yield a 25 x 1 binary vector used for training the perceptron [1111110101101011000100000" 100 10-2 1 1 2 2 N 10- 3 3 Squared error () ) flog scale] 4 4 4 106 s 5 5 5 4 5 3 4 1 2 4 5 5 2 3 (5) 3 (c) 10-8 10-10 100 Figure 2.31 (a) Original E character. (b) Modified version of the original character used for testing." (c) Another modified version of the original character used for testing. 10' 10 Number of iterations k [log scale) The perceptron learning rule given in (2.67) is used with a = 1 and the learning rate parameter set to u = 0.25. The desired neuron response is set to d = 0.5; that Square of the error at the neuron output versus is, this is a numerical value that identifies the character E after training is com- pleted, and the input pattern, the vector r shown above, is presented to the the iteration number during training. neuron. An error goal of 10- was established to terminate training. In other words, when the square of the difference between the desired response d and the actual response y is less than 10-, training of the neuron stops. The initial weights of the neuron were randomized, and after 39 presentations of the input pattern, the actual neuron output was y = 0.50009. Figure 2.32 shows the pro- gression of the neuron output error during training. One attractive feature of taking a neurocomputing approach for character recognition is the ability of the network to "correct" or compensate for inputs that can be corrupted by noise. In this example it is shown that the single neuron cannot correct for a noisy input: that is, alone it does not possess an error correction capability. For exam- ple, if the E is modified as shown in Figure 2.31(h), the resulting input to the single neuron yields an output of r = 0.5204. This is relatively close to the actual value that identifies a "true" E because the modified image looks similar to the E. However, there was no error correction carried out by the simple perceptron. Il the E is now modified as shown in Figure 2.31(c), the resulting neuron output is 1 = 0.6805, which is even further from the actual target value that identifies an E. The image in Figure 2.31(c) looks more like a C now: however, the neuron trained to only recognize an E has no idea what a C is supposed to "look like." Obviously more neurons are needed not only to allow for compensation of noisy inputs but also to recognize more characters. This can be accomplished with multilayer perceptrons (cf. Sect. 3.3). Also when we investigate the Hopfield associative memory (el. Sect. 5.3), it will be shown that this recurrent network has the cap- ability to compensate for noisy or incomplete inputs presented to it and to recog. size many different characters