i need to see solver equations

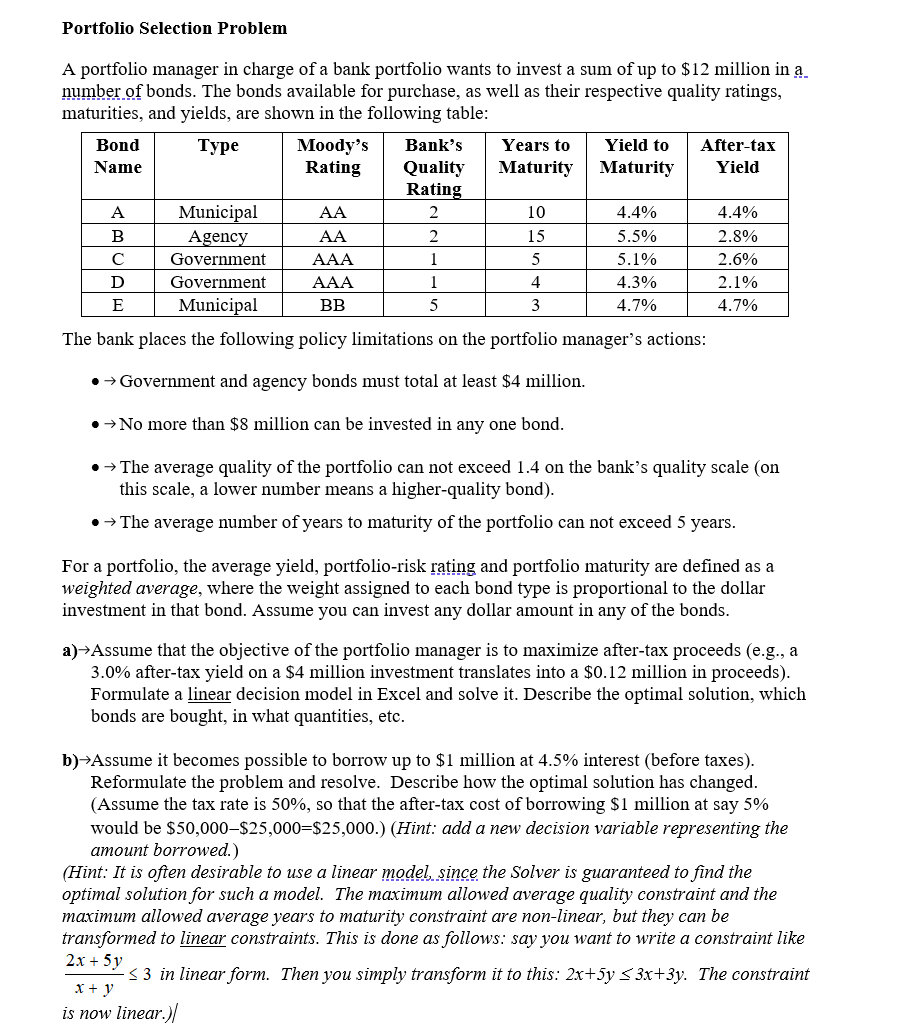
Portfolio Selection Problem A portfolio manager in charge of a bank portfolio wants to invest a sum of up to $12 million in _a_ numbengf bonds. The bonds available for purchase, as well as their respective quality ratings, maturities, and yields, are shown in the following table: Bond Type Moody's Bank's Years to Yield to Aftertax Name Rating Quality Maturity Maturity Yield Rating A Municipal AA 2 10 4.4% 4.40 B Agency AA 2 15 5.5% 2.8" C Government AAA 1 5 5. 1% 2.6% D Government AAA 1 4 4.3" 2.10 E Municipal BB 5 3 4. 7 4 .7\" The bank places the following policy limitations on the portfolio manager's actions: I -) Government and agency bonds must total at least $4 million. 0 -)No more than $8 million can be invested in any one bond. 0 -) The average quality of the portfolio can not exceed 1.4 on the bank's quality scale (on this scale, a lower number means a higher-quality bond). 0 -) The average number of years to maturity of the portfolio can not exceed 5 years. For a portfolio, the average yield, portfolio-risk rating and portfolio maturity are dened as a weighted average, where the weight assigned to each bond type is proportional to the dollar investment in that bond. Assume you can invest any dollar amount in any of the bonds. a]-)Assume that the objective of the portfolio manager is to maximize after-tax proceeds (e.g., a 3.0% after-tax yield on a $4 million investment translates into a $0.12 million in proceeds). Formulate a linear decision model in Excel and solve it. Describe the optimal solution, which bonds are bought, in what quantities, etc. b]-)Assume it becomes possible to borrow up to $1 million at 4.5% interest (before taxes). Reformulate the problem and resolve. Describe how the optimal solution has changed. {Assume the tax rate is 50%, so that the after-tax cost of borrowing $1 million at say 5% would be $50,000$25,000=$25,000.) (Hint: add a new decision variable representing the amount borrowed.) (Hint: It is often desirable to use a linear modeLsinge the Solver is guaranteed to find the optimal solution for such a model. The maximum allowed average quality constraint and the maximum allowed average years to maturity constraint are nonlinear, but they can be transformed to linear constraints. This is done as follows: say you want to write a constraint like 2.x - 5v x - y is now linear. )/ S 3 in linear form. Then you simply transform it to this: 2x+5y 53x+3y. T he constraint