I really need help making this function in Matlab. I would really appreciate help!

[f] = myFlowCalculator(S,d)

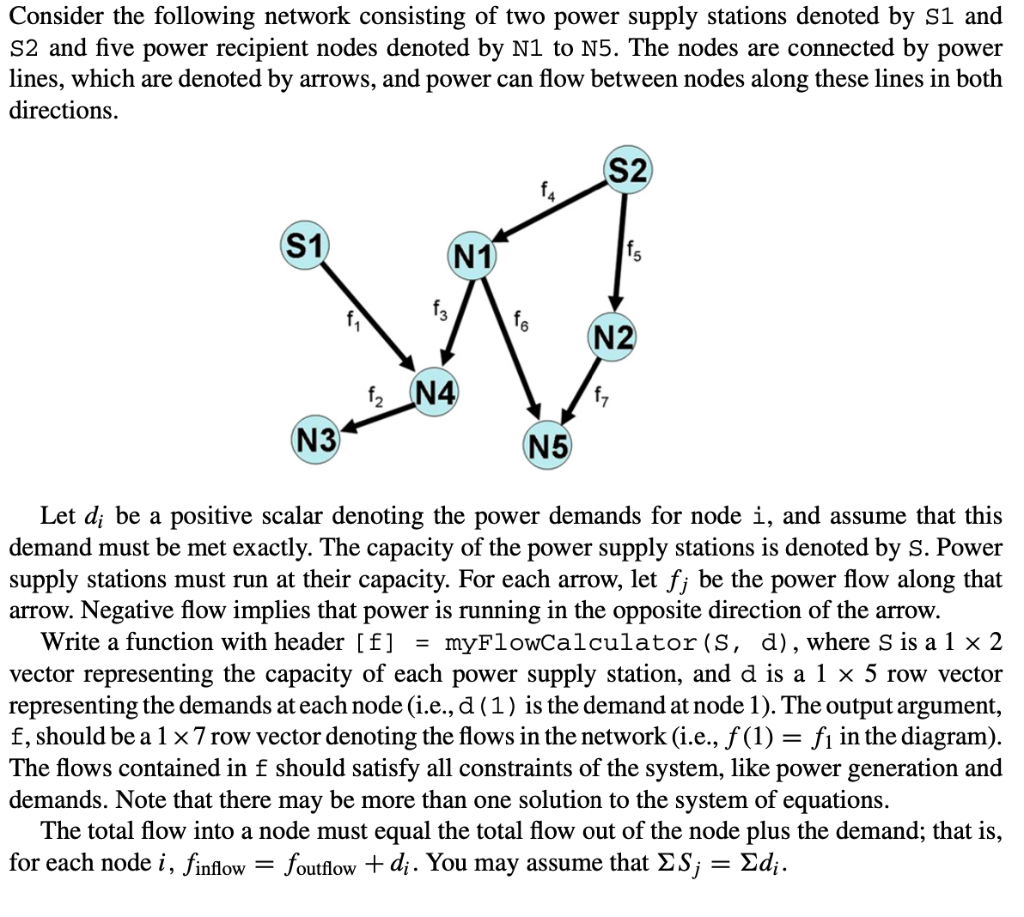
Consider the following network consisting of two power supply stations denoted by S1 and S2 and five power recipient nodes denoted by N1 to N5. The nodes are connected by power lines, which are denoted by arrows, and power can flow between nodes along these lines in both directions. S2 fa S1 N1 f5 f3 N2 fz_N4 f7 N3 N5 Let di be a positive scalar denoting the power demands for node i, and assume that this demand must be met exactly. The capacity of the power supply stations is denoted by S. Power supply stations must run at their capacity. For each arrow, let fj be the power flow along that arrow. Negative flow implies that power is running in the opposite direction of the arrow. Write a function with header [f] = myFlowCalculator(s, d), where S is a 1 x 2 vector representing the capacity of each power supply station, and d is a 1 x 5 row vector representing the demands at each node (i.e., d (1) is the demand at node 1). The output argument, f, should be a 1 x7 row vector denoting the flows in the network (i.e., f(1) = fi in the diagram). The flows contained in f should satisfy all constraints of the system, like power generation and demands. Note that there may be more than one solution to the system of equations. The total flow into a node must equal the total flow out of the node plus the demand; that is, for each node i, finflow foutflow + d. You may assume that ES; = Edi. Test Cases: >> f = myFlowCalculator ([10 10], [4 4 4 4 4]) f = 10.0000 4.0000 -2.0000 4.5000 5.5000 2.5000 1.5000 >> f = myFlowCalculator ([10 10), [3 4 5 4 4]) f = 10.0000 5.0000 -1.0000 4.5000 5.5000 2.5000 1.5000 Consider the following network consisting of two power supply stations denoted by S1 and S2 and five power recipient nodes denoted by N1 to N5. The nodes are connected by power lines, which are denoted by arrows, and power can flow between nodes along these lines in both directions. S2 fa S1 N1 f5 f3 N2 fz_N4 f7 N3 N5 Let di be a positive scalar denoting the power demands for node i, and assume that this demand must be met exactly. The capacity of the power supply stations is denoted by S. Power supply stations must run at their capacity. For each arrow, let fj be the power flow along that arrow. Negative flow implies that power is running in the opposite direction of the arrow. Write a function with header [f] = myFlowCalculator(s, d), where S is a 1 x 2 vector representing the capacity of each power supply station, and d is a 1 x 5 row vector representing the demands at each node (i.e., d (1) is the demand at node 1). The output argument, f, should be a 1 x7 row vector denoting the flows in the network (i.e., f(1) = fi in the diagram). The flows contained in f should satisfy all constraints of the system, like power generation and demands. Note that there may be more than one solution to the system of equations. The total flow into a node must equal the total flow out of the node plus the demand; that is, for each node i, finflow foutflow + d. You may assume that ES; = Edi. Test Cases: >> f = myFlowCalculator ([10 10], [4 4 4 4 4]) f = 10.0000 4.0000 -2.0000 4.5000 5.5000 2.5000 1.5000 >> f = myFlowCalculator ([10 10), [3 4 5 4 4]) f = 10.0000 5.0000 -1.0000 4.5000 5.5000 2.5000 1.5000