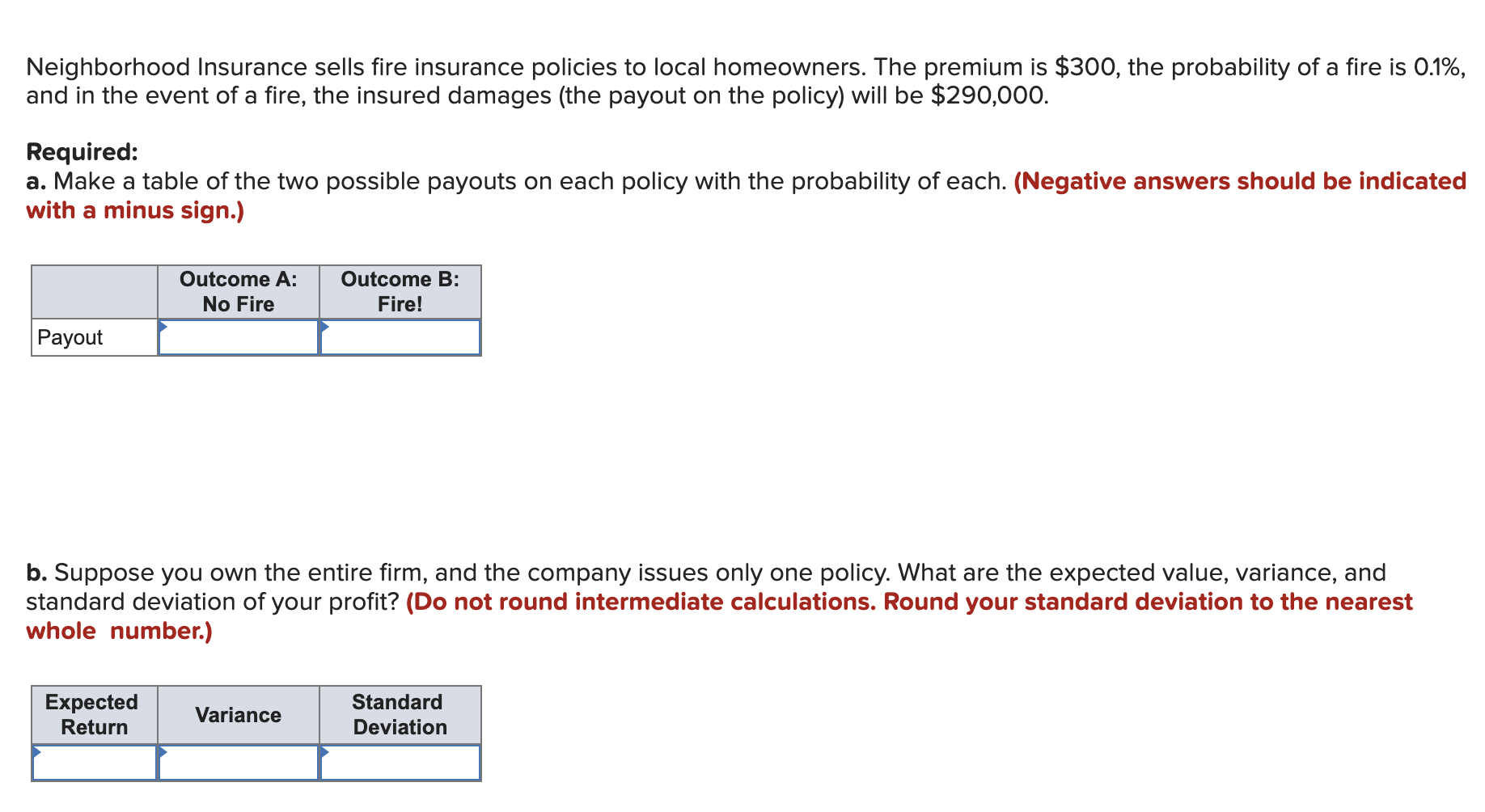
Question: I solved the problem, please give my attempts back. Solution : a. Payout, No Fire = $300 Payout, Fire = 300 + 290,000 = $289,700
I solved the problem, please give my attempts back.


Solution :
a. Payout, No Fire = $300 Payout, Fire = 300 + 290,000 = $289,700 b. Expected Return 290 + 300 = $10 Deviation From Mean 300 10 = $290 Squared Deviation 2902 = $84,100 Probability Deviation 84,100 x (1 0.001) = 84,016 Deviation From Mean $289,700 10 = $289,710 Squared Deviation 289,7102 = $83,931,884,100 Probability Deviation $83,931,884,100 x 0.001 = $83,931,884 Variance $84,016 + $83,931,884 = $84,015,900 Standard Deviation $84,015,900(1/2) = $9,166 c. Outcome, No Fire, Payout $300 2 = $600 Outcome, One Fire, Payout $600 $290,000 = $289,400 Outcome, Two Fires, Payout ($600 $290,000) 2 = $579,400 Probability, No Fire (1 0.001 0.001) = 99.8% Probability, One Fire (1 0.998 0.000001) = 0.001999 Probability, Two Fires 0.001 0.001 = 0.0001% d. Expected Return 1 99.8% 600 = $599 Expected Return 2 0.1999% $289,400 = 579 Expected Return 3 0.0001% $579,400 = $0 Expected Return 599 + 579 + 1 = 20 Deviation 600 20 = 580 Deviation $289,400 20 = 289,420 Deviation $579,400 20 = 579,420 Squared Deviation 580 580 = 336,400 Squared Deviation 289,420 289,420 = $83,763,936,400 Squared Deviation 579,420 579,420 = $335,727,536,400 P Sqdev 99.8% 336,400 = 335,727 P Sqdev 0.1999% $83,763,936,400 = $167,444,109.00 P Sqdev 0.0001% $335,727,536,400 = $335,728.00 Variance $335,727 + $167,444,109.00 + $335,728.00 = $168,115,564 Standard Deviation $168,115,564(1/2) = $12,966
e. Risk pooling increased the total variance of profit.
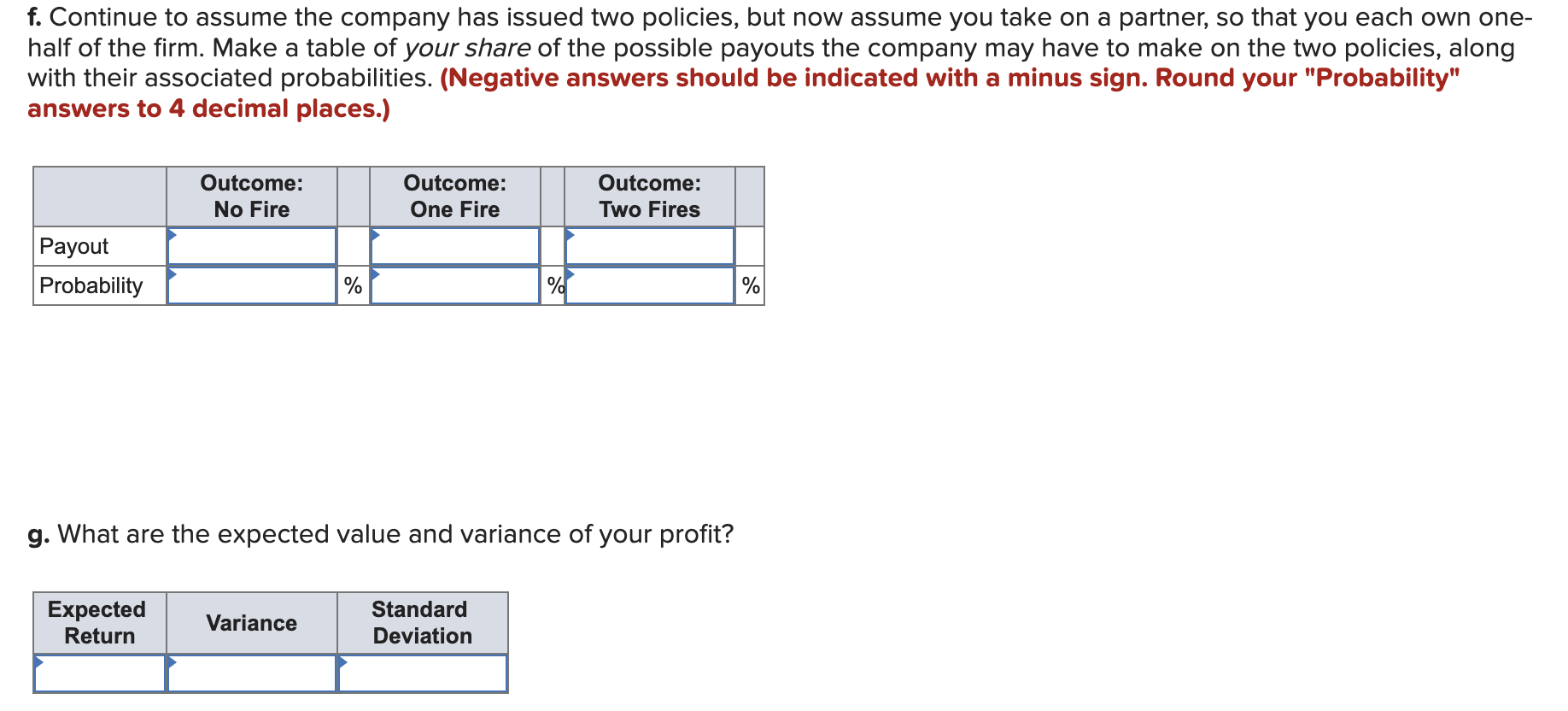
f. Payout, No Fire 300 Payout, One Fire (300 $290,000)/2 = $144,700 300 $290,000 = $289,700 Probability (1 0.001 0.001) = 99.8% Probability (1 0.998 0.000001) = 0.001999 Probability 0.001 0.001 = 0.0001% Expected Return 99.8% 300 = $300 Expected Return 0.1999% $144,700 = $289 Expected Return 0.0001% $289,700 = $0 Expected Return 299 + -289 + 0 = 10 Deviation 300 10 = 290 Deviation $144,700 10 = 144,710 Deviation 289,700 10 = 289,710 Squared Deviation 290 290 = 84,100 Squared Deviation 144,710 144,710 = 20,940,984,100 Squared Deviation 289,710 289,710 = 83,931,884,100 P X Sqdev 99.8% 84,100 = 83,932 P X Sqdev 0.1999% 20,940,984,100 = 41,861,027 P X Sqdev 0.0001% 83,931,884,100 = 83,932 Variance 83,932 + 41,861,027 + 83,932 = 42,028,891 Standard Deviation 42,028,891(1/2) = 6,483 h. Risk has dropped significantly while the expected profit is the same as (b). This demonstrates the power of Risk Sharing as a necessary complement to Risk Pooling. (g) is a superior outcome to (b) [Same Expected Reward, Lower Risk]. i. Risk Pooling builds both expected payout and variance. Risk Sharing implies profit sharing so expected payout is halved, but so has standard deviation.
Neighborhood Insurance sells fire insurance policies to local homeowners. The premium is $300, the probability of a fire is 0.1%, and in the event of a fire, the insured damages (the payout on the policy) will be $290,000. Required: a. Make a table of the two possible payouts on each policy with the probability of each. (Negative answers should be indicated with a minus sign.) b. Suppose you own the entire firm, and the company issues only one policy. What are the expected value, variance, and standard deviation of your profit? (Do not round intermediate calculations. Round your standard deviation to the nearest whole number.) c. Now suppose your company issues two policies. The risk of fire is independent across the two policies. Make a table of the three possible payouts along with their associated probabilities. (Negative answers should be indicated with a minus sign. Round your "Probability" answers to 4 decimal places.) d. What are the expected value, variance, and standard deviation of your profit? (Do not round intermediate calculations. Round your standard deviation to the nearest whole number.) e. Compare your answers to (b) and (d). Did risk pooling increase or decrease the variance of your profit? f. Continue to assume the company has issued two policies, but now assume you take on a partner, so that you each own onehalf of the firm. Make a table of your share of the possible payouts the company may have to make on the two policies, along with their associated probabilities. (Negative answers should be indicated with a minus sign. Round your "Probability" answers to 4 decimal places.) g. What are the expected value and variance of your profit? Neighborhood Insurance sells fire insurance policies to local homeowners. The premium is $300, the probability of a fire is 0.1%, and in the event of a fire, the insured damages (the payout on the policy) will be $290,000. Required: a. Make a table of the two possible payouts on each policy with the probability of each. (Negative answers should be indicated with a minus sign.) b. Suppose you own the entire firm, and the company issues only one policy. What are the expected value, variance, and standard deviation of your profit? (Do not round intermediate calculations. Round your standard deviation to the nearest whole number.) c. Now suppose your company issues two policies. The risk of fire is independent across the two policies. Make a table of the three possible payouts along with their associated probabilities. (Negative answers should be indicated with a minus sign. Round your "Probability" answers to 4 decimal places.) d. What are the expected value, variance, and standard deviation of your profit? (Do not round intermediate calculations. Round your standard deviation to the nearest whole number.) e. Compare your answers to (b) and (d). Did risk pooling increase or decrease the variance of your profit? f. Continue to assume the company has issued two policies, but now assume you take on a partner, so that you each own onehalf of the firm. Make a table of your share of the possible payouts the company may have to make on the two policies, along with their associated probabilities. (Negative answers should be indicated with a minus sign. Round your "Probability" answers to 4 decimal places.) g. What are the expected value and variance of your profit
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


