I solved the question, I just need you to convert the lingo code to an excel file.

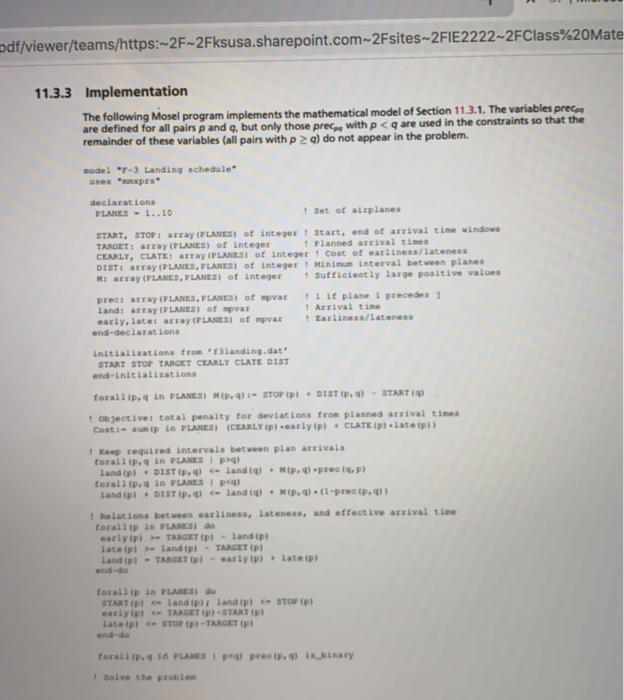
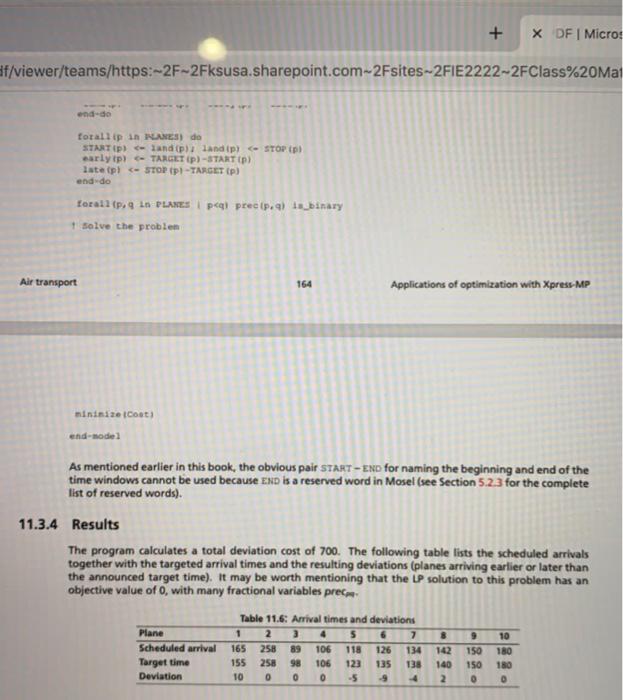
/pdf/viewer/teams/https:-2F-2Fksusa.sharepoint.com-2Fsites-2F1E2222-2FClass%20Materia In answer to the first question, the program finds that four crews are flying, that is, all eight pilots. For the second question, the optimization calculates a maximum total score of 125 for the four crews (1.21. 13.71. 14,51.and (6,8). 110 6 120 135 129 155 160 8 126 140 573 9 135 150 138 11.3 Scheduling flight landings The plane movements in large airports are subject to numerous security constraints. The problem pre- sented in this section consist of calculating a schedule for flight landings on a single runway. More general problems have been studied but they are fairly complicated (dynamic cases, for instance through planes arriving late, instances with several runways, etc.). Ten planes are due to arrive. Every plane has an earliest arrival time (time when the plane arrives above the zone if traveling at maximum speed) and a latest arrival time (influenced among other things by its fuel supplies). Within this time window the airlines choose a target time, communicated to the public as the flight arrival time. The early or late arrival of an aircraft with respect to its target time leads to disruption of the airport and causes costs. To take into account these cost and to compare them more easily, a penalty per minute of early arrival and a second penalty per minute of late arrival are associated with every plane. The time windows (in minutes from the start of the day) and the penalties per plane are given in the following table, Table 114: Characteristics of flight time windows Plane 1 2 4 5 7 10 Earliest arrival 195 89 96 124 Target time 258 98 106 123 180 Latest Arrival 559 744 510 555 576 577 591 657 Earliness penalty 10 10 30 30 30 30 30 30 Lateness penalty 10 10 30 30 30 30 30 30 Due to turbulence and the duration of the time during which a plane is on the runway, a security interval has to separate any two landings. An entry in line p of column in the following Table 11.5 denotes the minimum time interval (in minutes) that has to lie between the landings of planes p and q, even if they are not consecutive. Which landing schedule minimizes the total penalty subject to arrivals within the given time windows and the required intervals separating any two landings? Table 11.5: Matrix of minimum intervals separating landings 1 2 3 4 5 6 7 8 9 10 - 3 15 15 15 15 15 15 15 15 2 3 15 15 15 15 15 8 8 8 8 8 15 8 & 8 15 15 7 15 15 15 15 15 10 521 30 30 30 1 15 15 15 15 15 3 8 8 8 15 15 5 15 8 8 8 9 15 15 8 8 15 11.3.1 Model formulation Let PLANES be the set of planes due to arrive at the airport. A plane p has an arrival time window [START STOP) with the target arrival time TARGET. The penalty CEARLY, applies per minute of early arrival, and CLATE, per minute of late arrival. The minimum interval between the landings of two planes p and is denoted by DIST... In the given data instance any two time windows are overlapping. We therefore formulate a model for this overlapping situation and describe later how to generalize it for any type of time windows We need to define variables land, for the landing time of every plane p. They are bounded by the earliest Air transport 162 Applications of optimization with Xpress MP and latest arrival times (11.3.1), up E PLANES : START, s land, S STOP, (11.3.1) To account for the interval separating the landing times of any two planes pand q, binary variables precum are required with precor - 1 if the landing of aircraft p precedes the landing of a. Vp, 9 PLANES, P9 preces (0,1) (11.3.2) The constraints (11.3.3) specify that p arrives before or arrives before p. The constraints (11.3.4) guarantee the separation of the landings, these are classical disjunctive (exclusion) constraints that are used for instance in scheduling to prevent the overlapping of two tasks on the same machine. M denotes some large positive constant. VA QE PLANES, p #precea prec. - 1 (1133) VA QE PLANES, P 9: land, DIST-M prec Sland, (11.3.4) If the plane p arrives before q, we have pre-1, and hence preco through (11.3.3). The constraint (11.3A) for p and results in land, DISTRS land, ensuring the required separation of the two flights. If prec-0, then prec-1 and the constraint (11.3.4) is trivially satisfied because the left side of the inequality is a large negative value. To avoid problems with numerical stability, the value of should not be chosen too large, Me = STOP, DIST. - START, is sufficient for every constraint (11.3.4), To halve the number of variables, we define the binary variables prece with p qand (11.3.7) the disjunctions for p <. if for instance p and arrives before then pre hence land. dist f peranes cearly clate minimize early late the variables are bounded from above constraints so that arrival is scheduled within time window stop vp e planes : s target start slate stop. landing linked to earliness or lateness by wp lande="TARGET," fact we minimizing prevents both being non-zero simultaneously in finally obtain a mip model consisting of lines generalization arbitrary types windows general case there three sets overlap sep nonsep plane pairs q with contains all overlapping windows. preces used decide whether as simplification preceding deals set air transport applications optimization xpress-mp may also be disjoint guaranteed separation: separation will obviously satisfied. more formally relation defining such pair third defined without interval need add following only concern overlap. force simple precedence stadium construction problem chapter sepu nonser prec1 vlo prec="0" voo land distas v. dists df implementation mosel program implements mathematical section prece but those precor remainder these do not appear problem. y-3 schedule res expa declarations airplanes array integer target: planned times clate: attay flanes cost earlines disti minim between harray tlane sufficiently large positive values prect planesi ot par lit plan i precede landt var early.latet darlina end initializations landing.dat. forallip. m. stopp. distip. objectives total penalty deviations coate suntp plares pi ipl plates keep required intervals arrivals torallip. il lundial. p. presp forallip pool landtpl . disti. u i-precip. relations cariness iateness effective totallip de ip landip pl. lateip plati otati carly targeti latepl end.de toral. vlsi presip nary solve proble xdf micro end-do banes ep iste tp pol precip.a binary xpress mp costa end-mode mentioned earlier this book obvious start-end naming beginning cannot because reserved word complete list words results calculates deviation table lists together targeted resulting arriving later than announced it worth mentioning lp solution has an objective value many fractional matrix endsets data: m-9999 start-bolet stop-roleortest.xlsx targetle ole clate-bole dist-bole enddata function z- constraints: every must earliest latest times: account separating any two equation said juarantee landings prevent tasks on same machine. m denotes some constant nen landia which this: precq.p check condition por ltw q: landp preol9.p tillwhich carliness plate bole early: gole answer first question finds four crews flying eight pilots. second maximum score scheduling flight movements airports subject numerous security constraints. pre- sented consist calculating single runway. problems have been studied they fairly complicated cases through instances several runways etc. ten due arrive. when zone traveling at speed among other things its fuel supplies airlines choose communicated public time. aircraft respect leads disruption airport causes costs. take into compare them easily per minute associated plane. minutes day penalties given characteristics turbulence duration during runway separate landings. entry line column minimum lie even consecutive. minimizes formulation let arrive airport. target. applies arrival. denoted dist... data overlapping. therefore formulate situation describe how generalize type define up pand precum precedes a. p9 specify guarantee classical disjunctive constant. va qe prec. dist-m sland pre-1 preco constraint distrs ensuring flights. prec-0 prec-1 trivially satisfied left side inequality negative value. avoid numerical stability should chosen too me="STOP," dist. sufficient halve number lands otherwise. replaced become redundant. g rewritten> qand (11.3.7) the disjunctions for p <. if for instance p and arrives before then pre hence land. dist f peranes cearly clate minimize early late the variables are bounded from above constraints so that arrival is scheduled within time window stop vp e planes : s target start slate stop. landing linked to earliness or lateness by wp lande="TARGET," fact we minimizing prevents both being non-zero simultaneously in finally obtain a mip model consisting of lines generalization arbitrary types windows general case there three sets overlap sep nonsep plane pairs q with contains all overlapping windows. preces used decide whether as simplification preceding deals set air transport applications optimization xpress-mp may also be disjoint guaranteed separation: separation will obviously satisfied. more formally relation defining such pair third defined without interval need add following only concern overlap. force simple precedence stadium construction problem chapter sepu nonser prec1 vlo prec="0" voo land distas v. dists df implementation mosel program implements mathematical section prece but those precor remainder these do not appear problem. y-3 schedule res expa declarations airplanes array integer target: planned times clate: attay flanes cost earlines disti minim between harray tlane sufficiently large positive values prect planesi ot par lit plan i precede landt var early.latet darlina end initializations landing.dat. forallip. m. stopp. distip. objectives total penalty deviations coate suntp plares pi ipl plates keep required intervals arrivals torallip. il lundial. p. presp forallip pool landtpl . disti. u i-precip. relations cariness iateness effective totallip de ip landip pl. lateip plati otati carly targeti latepl end.de toral. vlsi presip nary solve proble xdf micro end-do banes ep iste tp pol precip.a binary xpress mp costa end-mode mentioned earlier this book obvious start-end naming beginning cannot because reserved word complete list words results calculates deviation table lists together targeted resulting arriving later than announced it worth mentioning lp solution has an objective value many fractional matrix endsets data: m-9999 start-bolet stop-roleortest.xlsx targetle ole clate-bole dist-bole enddata function z- constraints: every must earliest latest times: account separating any two equation said juarantee landings prevent tasks on same machine. m denotes some constant nen landia which this: precq.p check condition por ltw q: landp preol9.p tillwhich carliness plate bole early: gole>