I wanted to solve these two equations in python, but the program didn't work.

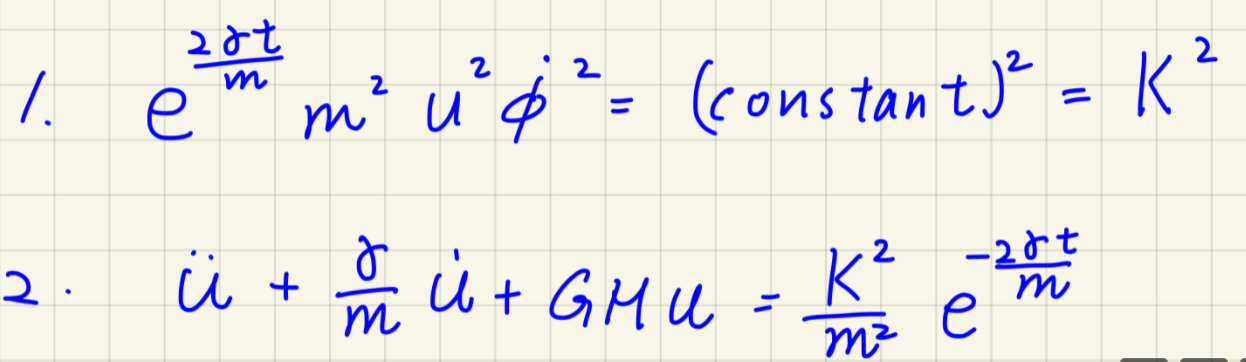and my code is below (it said: Repeated convergence failures (perhaps bad Jacobian or tolerances) Please tell me how to revise my code and solve these two differential equations.

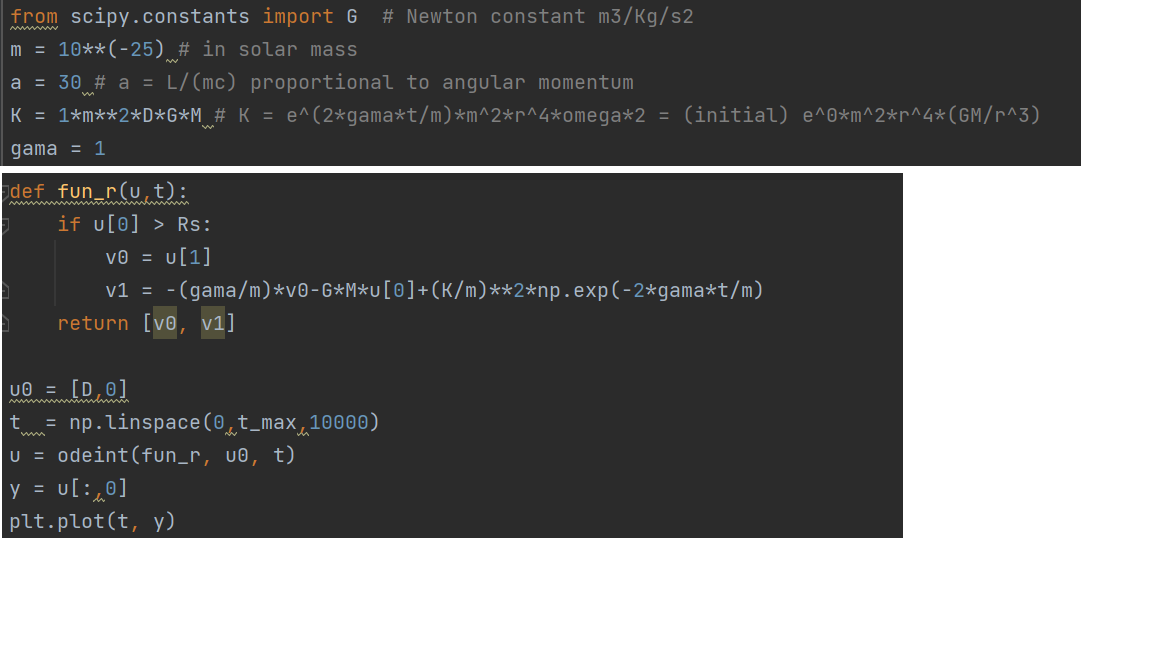
27t 2 2 2 m 2 7. e e ms? (constant)" - K? m ud 2 2 2 . + h i + GHU + K? -20t m e m ma from scipy.constants import G # Newton constant m3/Kg/s2 m = 10**(-25) # in solar mass a = 30 # a = L/(mc) proportional to angular momentum K = 1****2*D*G*M # K = e^(2xgama*t/m) *m^2*^4*omega*2 = (initial) e^0^m^2*^4*(GM/r^3) gama = 1 def fun_r(u,t): if u[o] > Rs: VO = u[1] v1 = -(gama/m) *v0-G*M*U[0]+(K/m)**2*np.exp(-2*gamaxt/m) return [vo, v1 t 10 = [D, 0] = np.linspace(0.xt_max_10000) U = odeint(fun_r, vo, t) y = [:0] plt.plot(t, y) 27t 2 2 2 m 2 7. e e ms? (constant)" - K? m ud 2 2 2 . + h i + GHU + K? -20t m e m ma from scipy.constants import G # Newton constant m3/Kg/s2 m = 10**(-25) # in solar mass a = 30 # a = L/(mc) proportional to angular momentum K = 1****2*D*G*M # K = e^(2xgama*t/m) *m^2*^4*omega*2 = (initial) e^0^m^2*^4*(GM/r^3) gama = 1 def fun_r(u,t): if u[o] > Rs: VO = u[1] v1 = -(gama/m) *v0-G*M*U[0]+(K/m)**2*np.exp(-2*gamaxt/m) return [vo, v1 t 10 = [D, 0] = np.linspace(0.xt_max_10000) U = odeint(fun_r, vo, t) y = [:0] plt.plot(t, y)