.i will ony accept answers with a good explanation

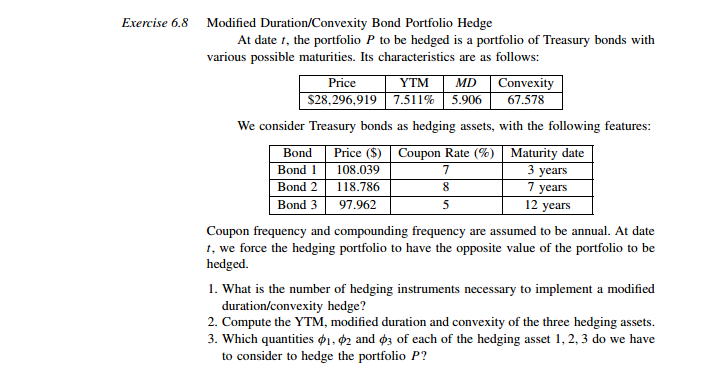
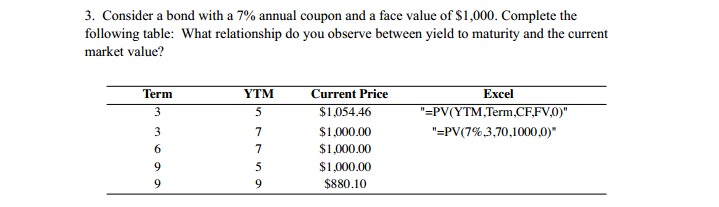
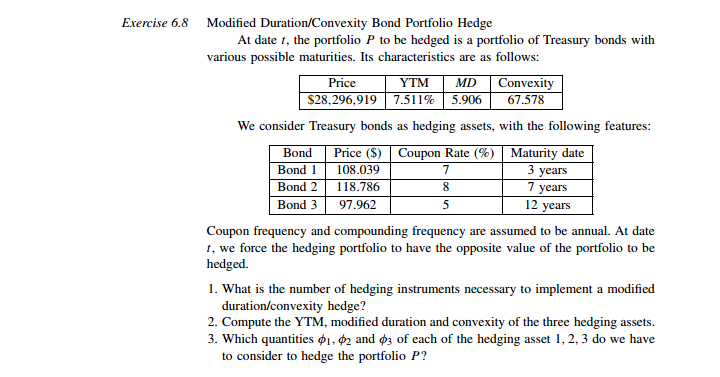
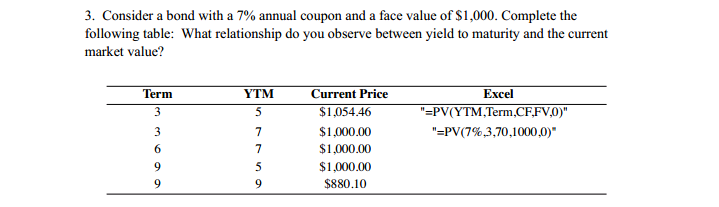
Exercise 6.6 Assume a 2-year Euro-note, with a $100,000 face value, a coupon rate of 10% and a convexity of 4.53. If today's YTM is 11.5% and term structure is flat. Coupon frequency and compounding frequency are assumed to be annual. 1. What is the Macaulay duration of this bond? 2. What does convexity measure? Why does convexity differ among bonds? What happens to convexity when interest rates rise? Why? 3. What is the exact price change in dollars if interest rates increase by 10 basis points (a uniform shift)? 4. Use the duration model to calculate the approximate price change in dollars if interest rates increase by 10 basis points. 5. Incorporate convexity to calculate the approximate price change in dollars if interest rates increase by 10 basis points.Exercise 6.8 Modified Duration/Convexity Bond Portfolio Hedge At date /, the portfolio P to be hedged is a portfolio of Treasury bonds with various possible maturities. Its characteristics are as follows: Price YTM MD Convexity $28,296,919 7.511% 5.906 67.578 We consider Treasury bonds as hedging assets, with the following features: Bond Price ($) Coupon Rate (%) Maturity date Bond 1 108.039 7 3 years Bond 2 118.786 7 years Bond 3 97.962 5 12 years Coupon frequency and compounding frequency are assumed to be annual. At date t. we force the hedging portfolio to have the opposite value of the portfolio to be hedged. 1. What is the number of hedging instruments necessary to implement a modified duration/convexity hedge? 2. Compute the YTM, modified duration and convexity of the three hedging assets. 3. Which quantities $1, $2 and 3 of each of the hedging asset 1, 2. 3 do we have to consider to hedge the portfolio P?3. The parameters of the Nelson and Siegel Extended model change instanta- neously to become Bo BI B2 B3 5.5% -1% 0.1% 5 2% 0.5 (a) Draw the new zero-coupon yield curve. (b) Compute the new price of the bond portfolio and compare it with the value given by the following equation: New Estimated Price = Former Price + ABo. Do, p + AB1 . DIP + AB2 . D2, p + AB3.D3.P where AB, is the change in value of parameter , and Dy,p is the $duration of the bond portfolio associated with parameter Bj. 4. Same questions when the coupon frequency is semiannual.Exercise 6.12 Bond Portfolio Hedge using the Nelson-Siegel Extended Model We consider the Nelson-Siegel Extended zero-coupon rate function RC (1, 0) = Bo + BI 1 - exp (- 7) 1 - exp (- ") + B2 exp ( - " ) 1 - exp (- 12) +B - exp 50 Problems and Solutions where R"(1, 0) is the continuously compounded zero-coupon rate at date f with maturity e. On 09/02/02, the model is calibrated, parameters being as follows: Bo BI B2 71 3 T2 5.9% -1.6% -0.5% 5 1% 0.5 At the same date, a manager wants to hedge its bond portfolio P against interest- rate risk. The portfolio contains the following Treasury bonds (delivering annual coupons, with a $100 face value): Bond Maturity Coupon Quantity Bond 1 01/12/05 4 10,000 Bond 2 04/12/06 7.75 10,000 Bond 3 07/12/07 4 10,000 Bond 4 10/12/08 7 10,000 Bond 5 03/12/09 5.7 10,000 Bond 6 10/12/10 5.5 10,000 Bond 7 01/12/12 4 10,000 Bond 8 03/12/15 4.75 10,000 Bond 9 07/12/20 4.5 10,000 Bond 10 |01/12/25 5 10.000 Bond 11 07/12/30 4.5 10,000 Bond 12 01/12/31 10,000 Bond 13 07/12/32 10,000 We consider Treasury bonds as hedging instruments with the following fea- tures: Hedging Asset Coupon Maturity Hedging Asset 1 4.5 04/15/06 Hedging Asset 2 5 12/28/12 Hedging Asset 3 6 10/05/15 Hedging Asset 4 6 10/10/20 Hedging Asset 5 6.5 10/10/31 Coupons are assumed to be paid annually, and the face value of each bond is $100. At date f, we force the hedging portfolio to have the opposite value of the portfolio to be hedged. 1. Compute the price and level, slope and curvature Sdurations of portfolio P. 2. Compute the price and level, slope and curvature Sdurations of the five hedging assets. 3. Which quantities $1, $2, $3, $4 and $5 of each hedging asset 1, 2, 3, 4 and 5 do we have to consider to hedge the portfolio P? 4. The parameters of the Nelson and Siegel Extended model change instanta- neously to become3. Consider a bond with a 7% annual coupon and a face value of $1,000. Complete the following table: What relationship do you observe between yield to maturity and the current market value? Term YTM Current Price Excel $1.054.46 "=PV(YTM,Term,CF,FV,0)" $1.000.00 "=PV(7%,3,70,1000,0)" DUNJU $1.000.00 $1.000.00 $880.1014. A bank has two, 3-year commercial loans with a present value of $70 million. The first is a $30 million loan that requires a single payment of $37.8 million in 3 years, with no other payments till then. The second is for $40 million. It requires an annual interest payment of $3.6 million. The principal of $40 million is due in 3 years. (a) What is the duration of the bank's commercial loan portfolio? (b) What will happen to the value of its portfolio if the general level of interest rates increased from 8% to 8.5%?QUESTIONS 1. The price value of a basis point will be the same regardless if the yield is increased or decreased by 1 basis point. However, the price value of 100 basis points (i.e., the change in price for a 100-basis-point change in interest rates) will not be the same if the yield is increased or decreased by 100 basis points. Why? The convex relationship explains why the price value of a basis point (i.e., the change in price for a 1-basis-point change in interest rates) will be roughly the same regardless if the yield is increased or decreased by 1 basis point, while the price value of 100 basis points will not be the same if the yield is increased or decreased by 100 basis points. More details are below. When the price-yield relationship for any option-free bond is graphed, it exhibits a convex shape. When the price of the option-free bond declines, we can observe that the required yield rises. However, this relationship is not linear. The convex shape of the price-yield relationship generates four properties concerning the price volatility of an option-free bond. First, although the prices of all option-free bonds move in the opposite direction from the change in yield required, the percentage price change is not the same for all bonds. Second, for very small changes in the yield required (like 1 basis point), the percentage price change for a given bond is roughly the same, whether the yield required increases or decreases. Third, for large changes in the required yield (like 100 basis points), the percentage price change is not the same for an increase in the required yield as it is for a decrease in the required yield. Fourth, for a given large change in basis points, the percentage price increase is greater than the percentage price decrease. 2. Calculate the requested measures in parts (a) through (f) for bonds A and B (assume that each bond pays interest semiannually). Needed bond details are below. Bond A Bond B Coupon 8% 9% Yield to maturity 8% 8% Maturity (years) 2 5 Par $100.00 $100.00 Price $100.00 $104.055 (a) What is the price value of a basis point for bonds A and B