I wonder WHY v x i cannot be .

Because I got v x i = (7i x i)+(4j x i)+(7k x i)= 7i^2+4ji+7ki and finally . But the answr is . HOW do I distinguish the order of i,j and k to figure out the positive or negative sign?

****I WONDER ONLY THIS PART****

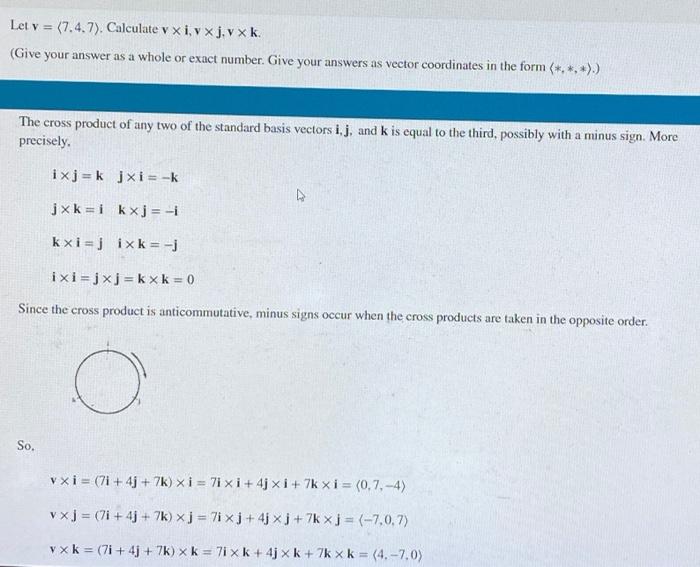
Let v = (7.4.7). Calculate v xi, vxj. vxk. (Give your answer as a whole or exact number. Give your answers as vector coordinates in the form (*.*.*>.) The cross product of any two of the standard basis vectors i, j, and k is equal to the third, possibly with a minus sign. More precisely ixj = k jxi= -k jxk=i kxj= -1 ki jix k = -1 ixi=jxj = kxk=0 Since the cross product is anticommutative, minus signs occur when the cross products are taken in the opposite order. So. vxi = (71+ 4 + 7k) Xi = 7ixi + 4 xi +7k xi = (0.7.-4) vx] = (71 +43 + 7k) xj = 7xj+4jxj+7kxj = (-7,0,7) vxk= (71+ 4j + 7k) x k = 71 x k +4jxk+ 7k x k = (4.-7.0)