I would like to know how to answer this question, it has to be done all in MATLAB and I'm new to it so I am having a hard time figuring out how it's done.

The natural logarithm function log_e(1 + x) can be approximated by the following formula 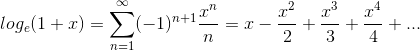for -1

(a) Write a function using for or while loop that computes an approximation to natural logarithm function log_e(1 + x) using the above formula. Your function must take x and n as function input arguments. n is the number of terms you want to keep in your approximation. The approximation will get more accurate if you keep more terms.

(b) Re-write your function using vectorization techniques.

(c) Determine the minimum number of terms you need to approximate log_e(0.5) = -0.69314718 to eight decimal digits? Print out your result on the screen as follows: "It takes n=1000 terms to approximate log(0.5) = -0.69314718 to six digits, the approximation is -0.693147179453401."

(d) Compute the error in the approximation to log(0.5) = -0.69314718 using n = 1, 5, 10, 25, 50, 100, 1000 terms in the above formula. Print a nice table of the results as follows:

n	Approximation	Error
1	-0.500000000000000	1.931471800000000e-01
5	...
10	...
25	...
50	...
100	...
1000	...

In g2z3 14 T" n+1 I--+-+-+... n