Iath $1$A

Definite Integrals are Everywhere

$2.$ Imagine at time $t=a$ we have a balance $P_0$ in a bank account with continuous compounding interest at a rate $r.$ If the balance at time $t$ is $P(t)$ then this means that $P^{\text{'}}(t)=rP(t)$ : Said concretely, $P(t)=P_0{e}^{r(t-a)}.$

Now, suppose we continuously add money to the account at a rate $f(t).$ If the initial balance is zero, we want to find the total amount in the account at time $T.$ We'll approximate continuous adding by discrete payments over smaller and smaller time intervals.

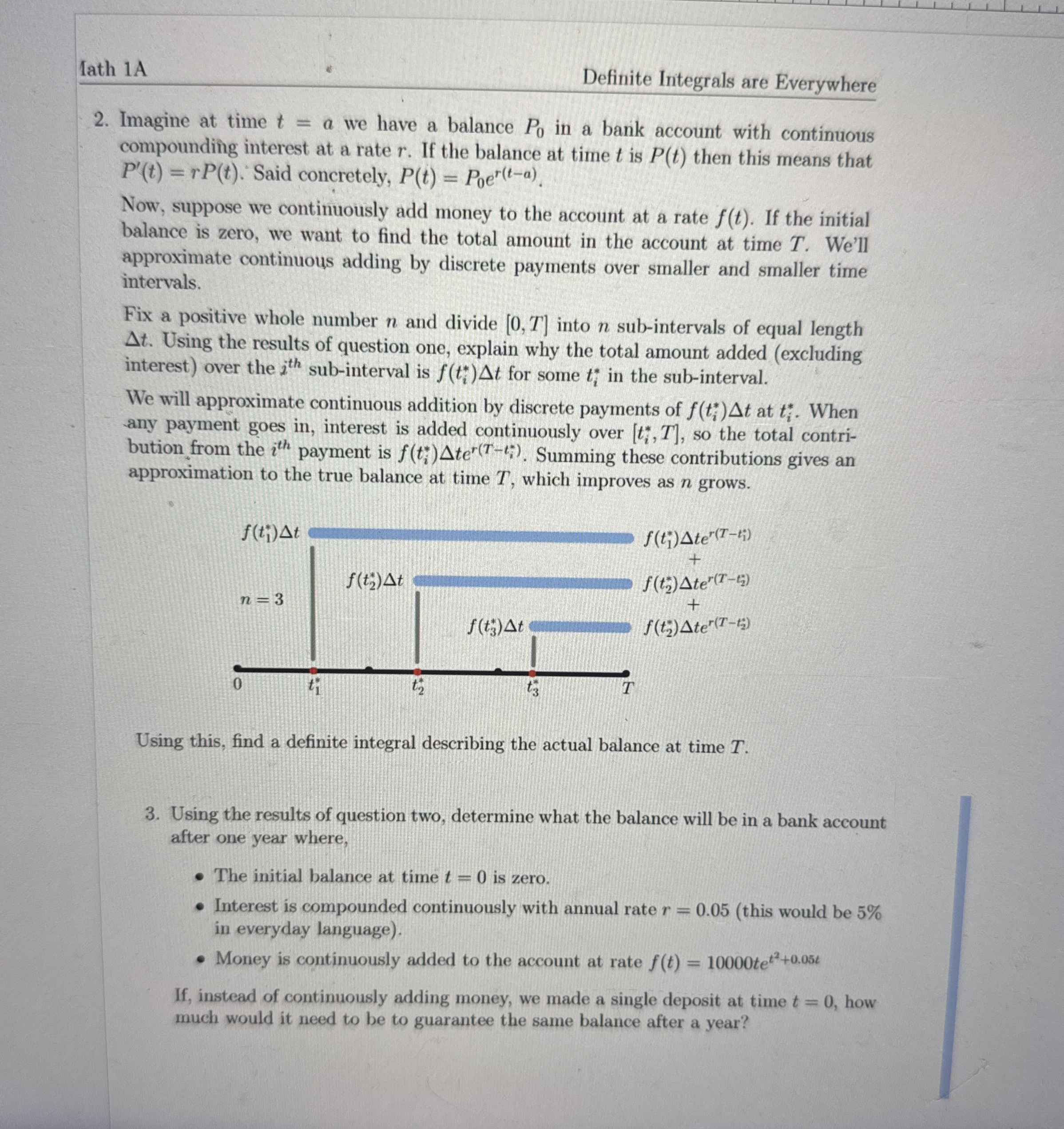
Fix a positive whole number $n$ and divide $0,T$ into $n$ sub$-$intervals of equal length $t.$ Using the results of question one, explain why the total amount added $($excluding interest$)$ over the $i^{th}$ sub$-$interval is $f(t_i^{**})t$ for some $t_i^{**}$ in the sub$-$interval.

We will approximate continuous addition by discrete payments of $f(t_i^{**})t$ at $t_i^{**}.$ When any payment goes in$,$ interest is added continuously over $t_i^{**},T,$ so the total contribution from the $i^{th}$ payment is $f(t_i^{**})t{e}^{r(T-t_i^{**})}.$ Summing these contributions gives an approximation to the true balance at time $T,$ which improves as $n$ grows.

$t{e}^{r(T-t_1)}$

$+$

$t{e}^{r(T-t_2)}$

$+$

$t{e}^{r(T-t_2)}$

Using this, find a definite integral describing the actual balance at time $T.$

$3.$ Using the results of question two, determine what the balance will be in a bank account after one year where,

The initial balance at time $t=0$ is zero.

Interest is compounded continuously with annual rate $r=0\mathrm{.}05($this would be $5\%$ in everyday language$).$

Money is continuously added to the account at rate $f(t)=10000t{e}^{t^2+0\mathrm{.}05t}$

If$,$ instead of continuously adding money, we made a single deposit at time $t=0,$ how much would it need to be to guarantee the same balance after a year?