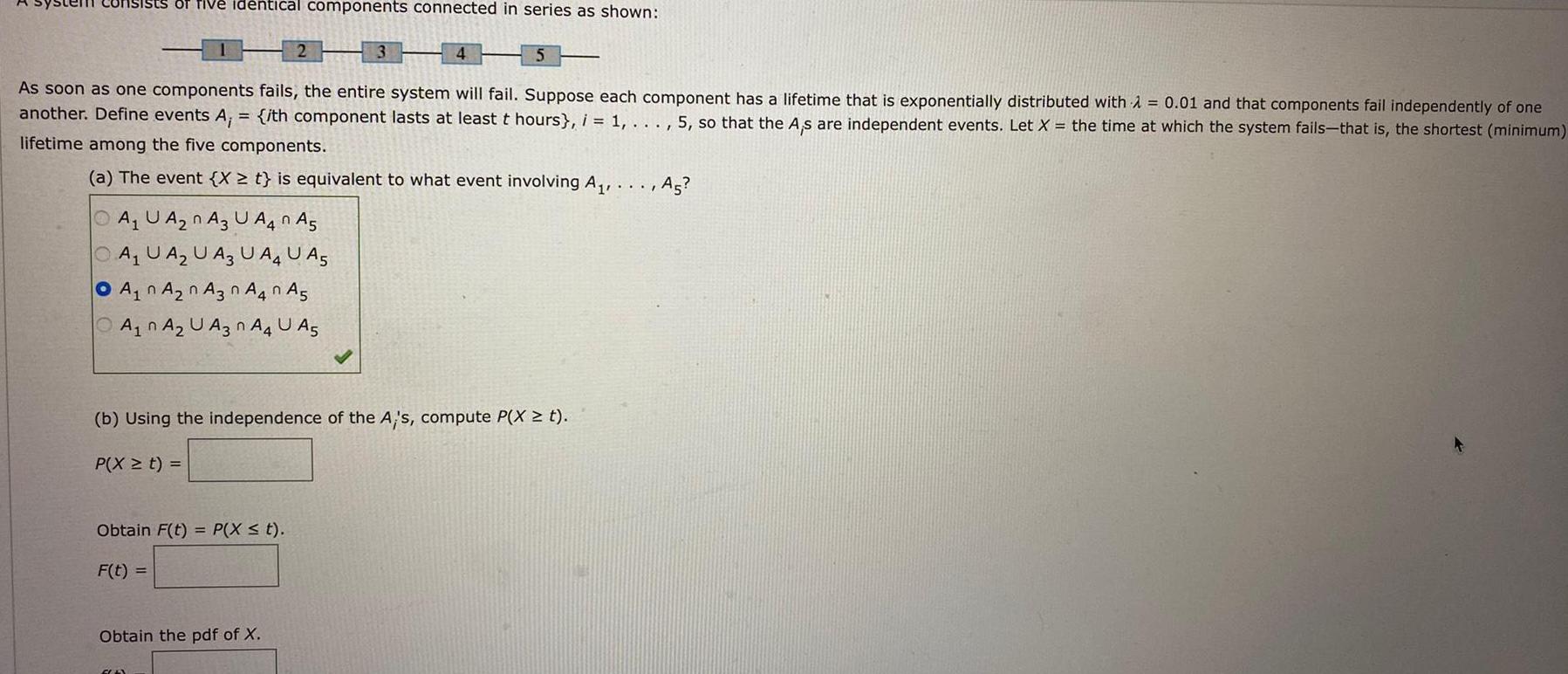
identical components connected in series as shown: 2 3 4 5 As soon as one components fails, the entire system will fail. Suppose each component has a lifetime that is exponentially distributed with = 0.01 and that components fail independently of one another. Define events A, = {ith component lasts at least t hours}, i = 1,..., 5, so that the A,s are independent events. Let X = the time at which the system fails-that is, the shortest (minimum) lifetime among the five components. (a) The event (X t) is equivalent to what event involving A, OA, UAn A3 UA4n As OAUAUA UA4 UAS A1 A2 A3 A4 A5 An A UA3 A4 A5 , As? (b) Using the independence of the A's, compute P(X t). P(X t) = Obtain F(t) = P(X t). F(t) = Obtain the pdf of X.