Question: If A and B are both second-order tensors and t, u, v, and w are all vectors, prove the following identities using the indicial

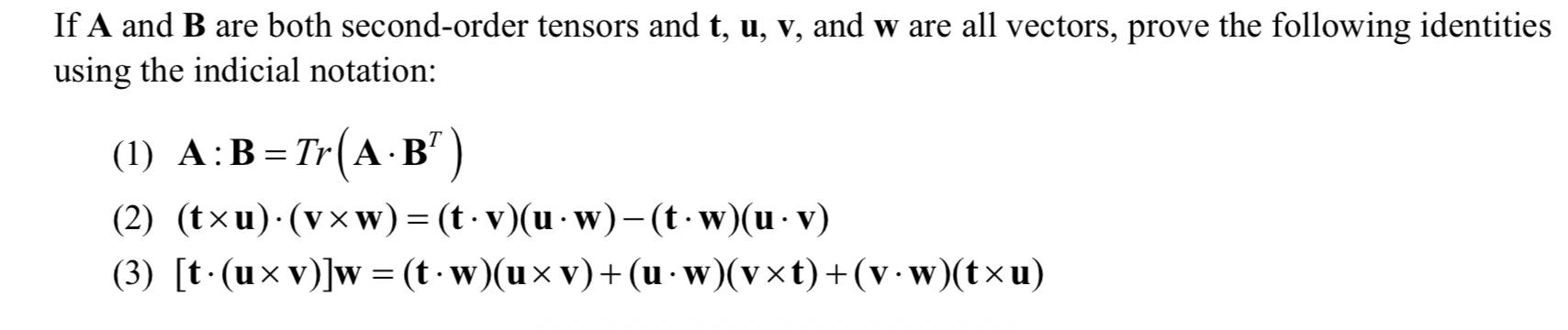
If A and B are both second-order tensors and t, u, v,

If A and B are both second-order tensors and t, u, v, and w are all vectors, prove the following identities using the indicial notation: (1) A:B=Tr( AB' Tr(AB") (2) (txu)(vw) = (t - v)(u w)-(tw)(u v) (3) [t(uxv)]w = (t w)(u v)+ (u - w)(vt)+(v w)(tu)

Step by Step Solution

★★★★★

3.54 Rating (151 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Sol Given A B are both Second order ten... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

If A and B are vectors specified in magnitude-direction form, and C = A + B is to be found and to be expressed in magnitude-direction form, how is this done? That is, what is the procedure for adding...

Prove that if A and B are skew-symmetric n n matrices, then so is A + B.

Prove that if A and B are n n matrices, then tr (AB) = tr (BA).

(a) Find an orthogonal matrix Q and a diagonal matrix Î such that K = Q Î QT. (b) Is K positive definite? (c) Solve the second order system d2u/t2 = A u subject to the initial conditions...

Answer Exercise 9.5.17 when In Exercise 9.5.17 (a) Find an orthogonal matrix Q and a diagonal matrix Î such that K = Q Î QT. (b) Is K positive definite? (c) Solve the second order system...

The research and development team of a medical device manufacturer is designing a new diagnostic test strip to detect the breath alcohol level. The materials used to make the device are listed here...

From a management perspective, formulate and explain your company's offensive or defensive strategy to improve its market position in the next 3 years. Explain whether your company will be a first...

While performing a simulation of a single-server queueing system, the number of customers in the system is 0 for the first 10 minutes, 1 for the next 17 minutes, 2 for the next 24 minutes, 1 for the...

Let w be the weight (in pounds) of a woman who weighs between 140 and 145 pounds. Describe the womans weight using inequality notation, interval notation, and a graph.

At an intersection of hospital hallways, a convex mirror is mounted high on a wall to help people avoid collisions. The mirror has a radius of curvature of 0.550 m. Locate and describes the image of...

Describe an incident when you had to listen attentively to act quickly enough to meet a deadline. What active listening skills did you demonstrate? If you had to do it over again, would you do...

Evaluate the surface integral F d S where F = ( x , 2 y , 3 z ) and S i s the cube with vertices a t ( + - 1 , + - 1 , + - 1 )

A uniform ladder is 10 m long and weighs 200 N. In Figure the ladder leans against a vertical, frictionless wall at height h = 8.0 m above the ground. A horizontal force F is applied to the ladder at...

A small object is attached to the end of a string to form a simple pendulum. The period of its harmonic motion is measured for small angular displacements and three lengths, each time clocking the...

As shown in Fig. P2.44, the 6-in-thick exterior wall of a building has an average thermal conductivity of 0.32Btu/h ft oR. At steady state, the temperature of the wall decreases linearly from T1 =...

Expectant parents are thrilled to hear their unborn babys heartbeat, revealed by an ultrasonic motion detector. Suppose the fetuss ventricular wall moves in simple harmonic motion with amplitude of...

Customers are used to evaluate preliminary product designs. In the past, 95% of highly successful products received good reviews, 60% of moderately successful products received good reviews, and 10%...

Two loudspeakers emit sound waves along the x-axis. The sound has maximum intensity when the speakers are 25 cm apart. The sound intensity decreases as the distance between the speakers is increased,...

Hello ther, I need help with my finance case study (Ramsey Co. Case study). Please see the attachments for details and instructions. Thanks, Ramsey Inc. 2013 Purchase Order Register March 1, 2013 -...

1.Is there a relationship between a student's Language Arts Scaled Score (cstlass) and a student's Math Scaled Score (cstmss)? id 11:213141516171819/10i1 1:12:13:14:15/16/17/18prtcorrproflviproftxt...

A researcher at a marketing firm examines whether the age of a consumer matters when buying athletic clothing. Her initial feeling is that Brand A attracts a younger customer, whereas the more...

1. Research has shown that the relationship between eye contact and deception a. is nonexistent b. is positive in that eye contact increases as the level of deception rises c. is negative in that eye...

A. Sales Records 1. Format the sales records dataset as a table. Make sure the table columns are wide enough to fit the column contents. 2. Sort the sales records by Region first in a custom order of...

The introduction provides a succinct summary of all of the following: the management issue the focus of the three journal articles the three recommendations A comprehensive explanation of a single...