Question: If B is given to be any arbitrary mxn matrix and if D is given to be any mxm symmetric matrix then show/prove that K=(B^T)DB

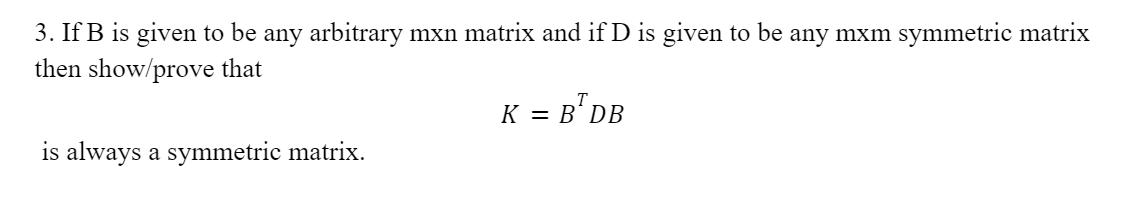
If B is given to be any arbitrary mxn matrix and

If B is given to be any arbitrary mxn matrix and if D is given to be any mxm symmetric matrix then show/prove that

K=(B^T)*D*B

is always a symmetric matrix.

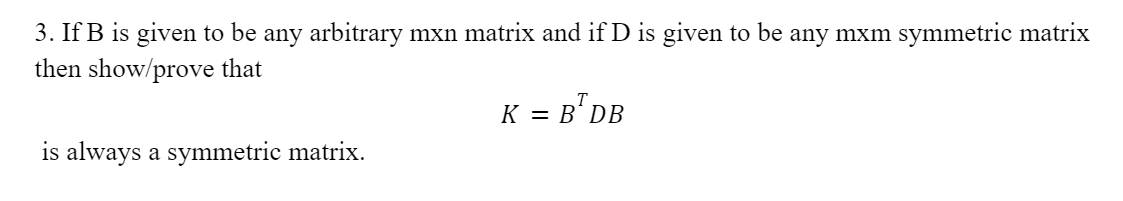
3. If B is given to be any arbitrary mxn matrix and if D is given to be any mxm symmetric matrix then show/prove that K = BTDB is always a symmetric matrix

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Questions: 54. The rank of a matrix is defined as the maximum number of : (a) linearly independent rows of a matrix (b) linearly independent columns of a matrix (c) both a & b (d) neither a nor b 55....

*How to limit clubs in your community. Suppose there are n people in your community and the community leaders are feeling overwhelmed by the number of different clubs that are getting formed (for...

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

Show the parse trees for the two parses that the grammar assigns for sentence S1. S1: the train station bus rumbles [3 marks] (b) Give an algorithm for a bottom-up passive chart parser without...

software projects failed. In the run-up to Y2K, most of the world's large companies claimed that fixing the Millennium Bug was a large project whose success was critical to their survival. One would...

re Regular Languages and Finite Automata (a) Let L be the set of all strings over the alphabet {a, b} that end in a and do not contain the substring bb. Describe a deterministic finite automaton...

I have done every one except for part i and j. Please help me with just those two parts! Thanks! Write a test program that uses BMat objects to do specified Boolean matrix calculations. The starting...

350 Specification and Verification II Explain how a register can be modelled either as a unit-delay, or with an explicit clock input. [4 marks] Describe the relationship between the two models. [4...

1 Distributed Systems In a distributed electronic conference application each participant has a replica of a shared whiteboard. Only one user at a time may write to the whiteboard, after which the...

Write a test program that uses BMat objects to do specified Boolean matrix calculations. The starting version of your program should be the sample file P4Test.java . Instance BMat objects for the...

Starting with Eqs (4.35) and (4.43), derive Eq. (4.62).

5. Consider a standalone, single-user Java application which acts as a basic electronic English dictionary. A user of this application: typically searches for the meanings of an English word, and ...

a . e x e x - 1 2 d x b . e x 1 - e 2 x 2 d x c . 1 e x - 1 2 d x

At the beginning of the year, the stockholders equity section of the balance sheet of Solutions Corporation reflected the following: Common stock (par $12; authorized 65,000 shares, outstanding...

The records of Hollywood Company reflected the following balances in the stockholders equity accounts at December 31, 2010: Common stock , par $12 per share, 30,000 shares outstanding Preferred...

Do most researchers still insist on at least interval level of measurement as a condition for the use of parametric statistics?

The bitter, eight-month baseball strike that ended the 1994 season so abruptly was expected to have substantial repercussions at the box office when the 1995 season finally got under way. It did. By...

During 2014 the following selected transactions affecting stockholders equity occurred for Orlando Corporation: Apr. 1 Purchased in the market 200 shares of the companys own common stock at $20 per...

Tori and some other childeen experimented with balls to see which ones rolled. First using a piece of cardboard to use as a ramp, they angled it on a block to the floor to test the balls. Then Tori...

a. If everyone thinks that the price of tomatoes will go up next week, what is likely to happen to demand for tomatoes today? b. If everyone thinks that the price of gasoline will go up next week,...

When the price of Apple computers goes down, what probably happens to the demand for Windows-based computers? pg74

Suppose the table below shows the number of labor hours needed to produce airplanes and automobiles in the United States and South Korea, but one of the numbers is unknown. pg86 a. Without knowing...

Question: If B is given to be any arbitrary mxn matrix and if D is given to be any mxm symmetric matrix then show/prove that K=(B^T)*D*B

Step by Step Solution

Students Have Also Explored These Related Mathematics Questions!

Question: If B is given to be any arbitrary mxn matrix and if D is given to be any mxm symmetric matrix then show/prove that K=(B^T)DB