Question: If d is a metric on a vector space X = {0} which is obtained from a norm || ||, and d is defined

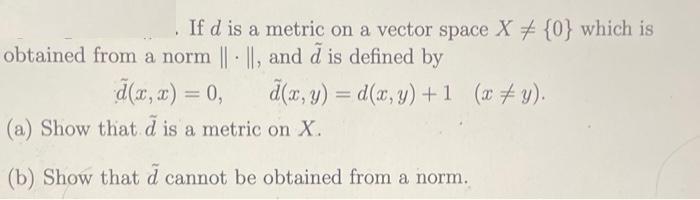
If d is a metric on a vector space X = {0}

If d is a metric on a vector space X = {0} which is obtained from a norm || ||, and d is defined by d(x, y) = d(x, y) + 1 (x+y). d(x,x) = 0, (a) Show that d is a metric on X. (b) Show that d cannot be obtained from a norm.

Step by Step Solution

★★★★★

3.44 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The search results provide insights into metric spaces and Dmetric spaces A metric on a set X is def... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

A thermodynamic system is taken from stare a to state c in Fig. 19.29 along either path abc or path adc. Along path abc, the work W done by the system is 450 J. Along path adc, W is 120 J. The...

A metric space is connected if and only it cannot be represented as the union of two disjoint closed sets.

Vector Space Properties: Show that the properties in Problems 1-3 hold in any vector space? 1. Unique Zero: The zero element in a vector space is unique. Start with two zero elements and show that...

Variable and Absorption Costing are two alternative methods of determining product costs. Discuss why a company would choose variable costing over absorption costing. Include how the Income Statement...

Prof. ll June 14, 2016 MAT224: Differential Equations Existence and Uniqueness of Solutions Consider the Initial Value Problem: y (x) = f (x, y) y(x0 ) = y0 . It would be good to know if a solution...

Linear Algebra Final answer only please Section 3.2 Subspaces: Problem 1 (1 point) ATTEMPT NOT ACCEPTED - Please submit answers again (or request new version if necessary). Determine which of the...

Answer all the question 1b, including 1b(ii) and 1b(iii). b(ii) Show that de and d|E are topologically equivalent metrics on E . b(iii) Show that (E, d) is a complete metric space. You can use the...

Answer the questions. in the following attachments. Question 1. (10 marks) Consider the function z = f(x, y) = x/y. Showing all steps, use the Newton Quotient approach to find ?z/?y. Question 2. (5...

5. Let K be a compact set on the metric space (X,d) and g: X > R continuous functions such that 9(93) > 0 and f(93) > 0 for all x E K. (a) Show that there exist positive constants Cl, 02 such that...

Given in the below table, Income and Consumption based on which you are required to ascertain the following 1. Average Propensity to Consume 2. Average Propensity to Save 3. Marginal Propensity to...

Preston Toy Co. has warrants outstanding that allow the holder to purchase a share of stock for $22 (exercise price). The common stock is currently selling for $28, while the warrant is selling for...

Set up T accounts for each of the general ledger accounts needed for the following transactions. Invested cash in the business, $4,400. Paid office rent, $500. Purchased office supplies on account,...

Which statements are TRUE regarding BDCs ? I BDCs invest in securities of publicly traded companies II BDCs make direct investments in privately - held companies III BDCs are publicly traded IV BDCs...

Read Frank Abagnales book, Catch Me If You Can. Prepare a report on the nature and level of complexity of his fraudulent schemes. What, in your opinion, made them so successful?

Is there a relationship between a students GPA and the number of pencils in his or her backpack? Jordynn and Angie decided to find out by selecting a random sample of students from their high school....

Your client, Alternate Fuel, Inc. (a regular corporation), owns three sandwich shops in the Philadelphia area. In 2016, the year Alternate Fuel incorporated, it acquired land on the outskirts of...

Liquid water is heated, so it becomes superheated vapor. Can specific heat be used to find the heat transfer? Explain.

Describe one of the safety committees your organization uses and how it reduces risk within your organization. Who are the general members of the group, how often do they meet, and is there a...

What is the largest order among the orders of all the cyclic subgroups of Z 6 x Z 8 ? of Z 12 x Z 15 ?

Compute the given arithmetic expression and give the answer in the form a + bi for a, b R. i 4

Deal with showing the uniqueness of the prime powers appearing in the prime-power decomposition of the torsion subgroup T of a finitely generated abelian group. Using Exercise 17, show that provided...

Prepare a master schedule like that shown in Figure given this information: The forecast for each week of an eight- week schedule is 50 units. The MPS rule is to schedule production if the projected...

What factors can create safety stock requirements in an MRP system?

Contrast planned- order receipts and scheduled receipts.