If f and g are the functions whose graphs are shown, let u(x)=f(g(x)), v(x)=g(f(x)), and w(x)=g(g(x)). Find each derivative, if it exists. If not explain why.

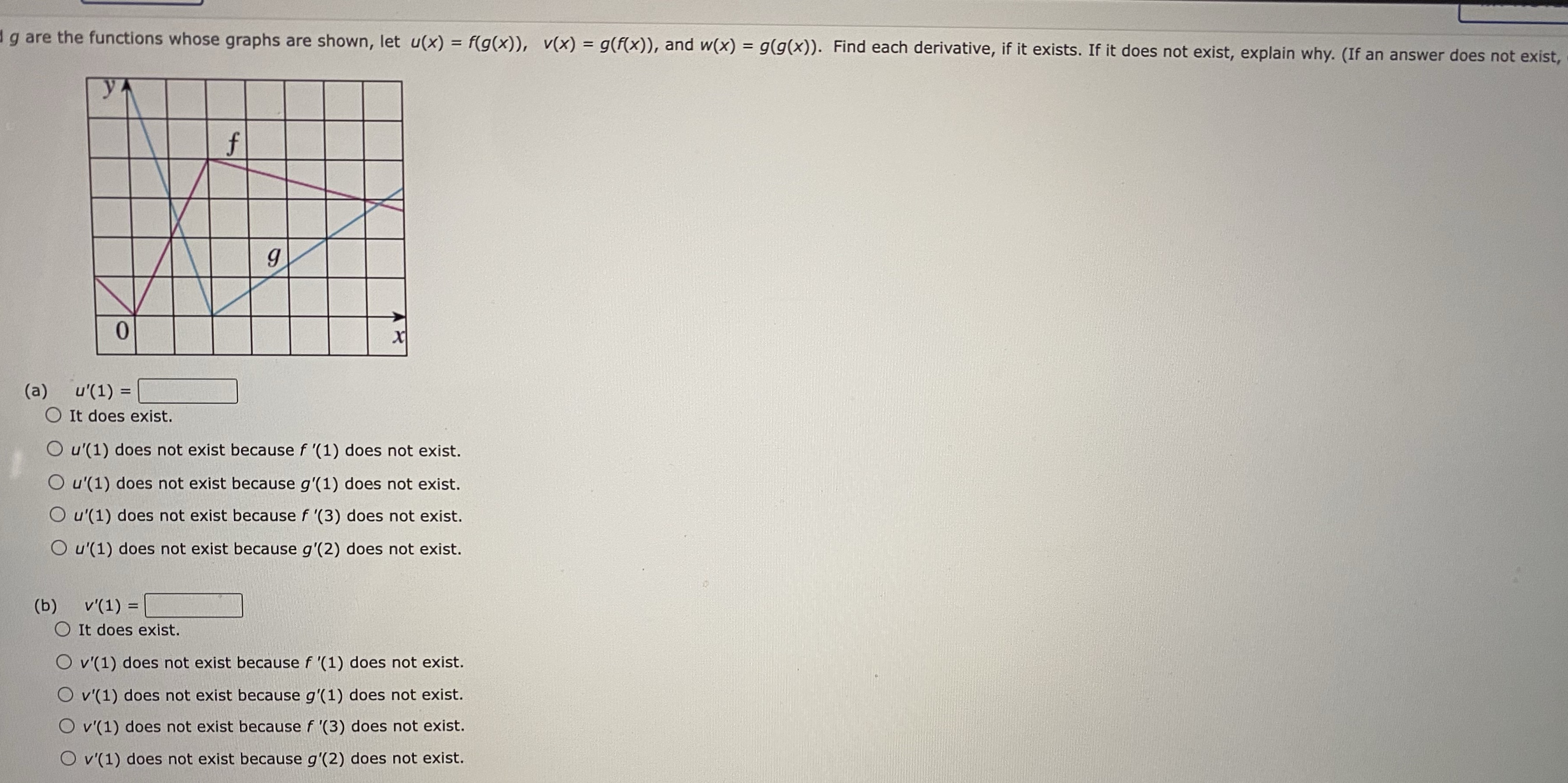
g are the functions whose graphs are shown, let u(x) = f(g(x)), v(x) = g(f(x)), and w(x) = g(g(x)). Find each derivative, if it exists. If it does not exist, explain why. (If an answer does not exist, f (a) u'(1 ) = O It does exist. O u'(1) does not exist because f '(1) does not exist. O u'(1) does not exist because g'(1) does not exist. O u'(1) does not exist because f '(3) does not exist. O u'(1) does not exist because g'(2) does not exist. (b ) v' ( 1 ) = [ It does exist. O v'(1) does not exist because f '(1) does not exist. O v'(1) does not exist because g'(1) does not exist. O v'(1) does not exist because f '(3) does not exist. O v'(1) does not exist because g'(2) does not exist