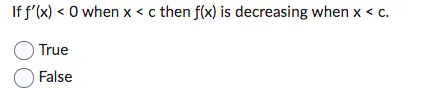
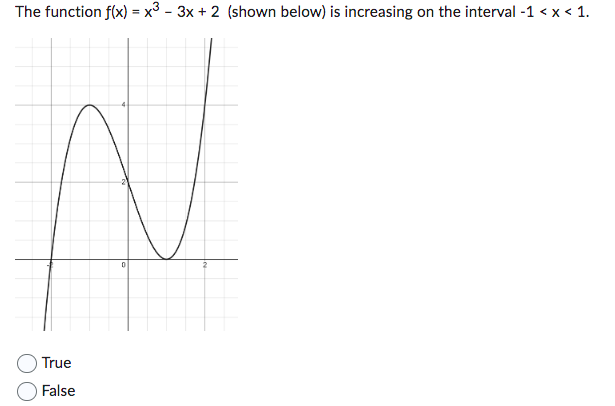
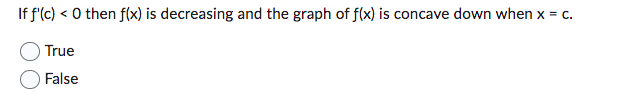
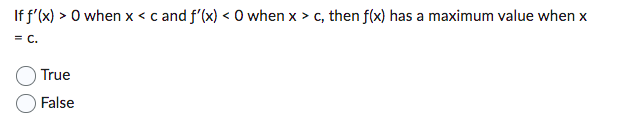
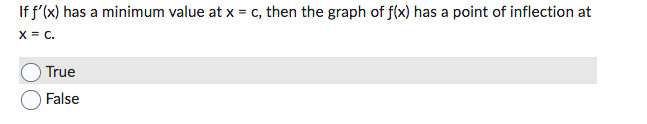
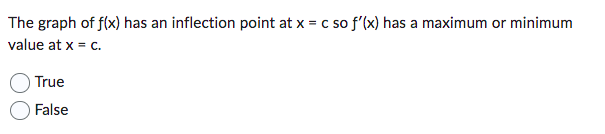
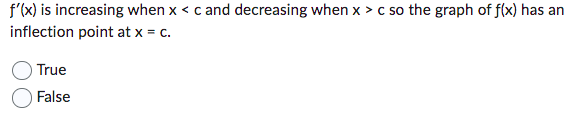
If f'(x) < 0 when x < c then f(x) is decreasing when x < c. True False The function f(x) = x-3x+2 (shown below) is increasing on the interval -1 < x < 1. True False 0 If f'(c) < 0 then f(x) is decreasing and the graph of f(x) is concave down when x = c. True False A local extreme point of a polynomial function f(x) I can only occur when f'(x) = 0. True False If f'(x) > O when x If f'(x) has a minimum value at x = c, then the graph of f(x) has a point of inflection at x = c. True False If f'(c) > 0 and f"(c) > 0, then f(x) is increasing and the graph is concave up when x = C. True False If f'(c) = 0 then f(x) must have a local extreme point at x = c. True False The graph of f(x) has an inflection point at x = c so f'(x) has a maximum or minimum value at x = c. True False f'(x) is increasing when x < c and decreasing when x > c so the graph of f(x) has an inflection point at x = c. True False