If someone could explain this question and solution for an exam that would be amazing. Where are $2.75 and $102.75 cash flows coming from? I get the 102.75 is 100+2.75 but where is the 2.75 coming from?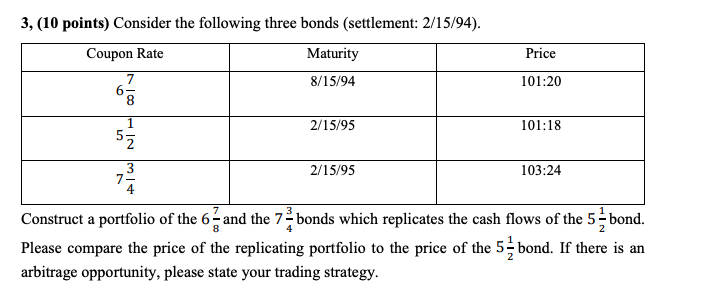

3, (10 points) Consider the following three bonds (settlement: 2/15/94). Coupon Rate Maturity 8/15/94 Price 101:20 2/15/95 101:18 2/15/95 103:24 Construct a portfolio of the 6- and the 7 bonds which replicates the cash flows of the 5-bond. Please compare the price of the replicating portfolio to the price of the 5- bond. If there is an arbitrage opportunity, please state your trading strategy. 3, It is helpful as we begin to list the 8/15/94 and 2/15/95 cash flows of the bond we are replicating: Cash Flow 8/15/94 2.75 2/15/95 102.75 For simplicity, I will rename the bonds as follows: 67 Bond A; 7 Bond B; 5 Bond C. I will use A to represent the number of units of Bond A in the replicating portfolio and B to represent the number of units of Bond B in the replicating portfolio. So we have: ax(1004 10 **) + 2 x 10 x 275 ox(100+100 x+3) = 10275 Solving them, we have B = 0.9892 and A = -0.0105. That is, we buy 0.9892 of Bond B, and we sell short 0.0105 of Bond A. To see whether there is arbitrage opportunity, we need to calculate the price of the replicating portfolio and compare it with the price of the bond we are replicating: Price of Replicating Portfolio = 0.9892 x 1034 0.0105 x 101m0 = 101.5623 Price of Bond C = 101 13 = 101.5625 Since the replicating portfolio is cheaper, we can buy the replicating portfolio and sell short one unit of Bond C. Doing this, we can capture $0.0002 per transaction