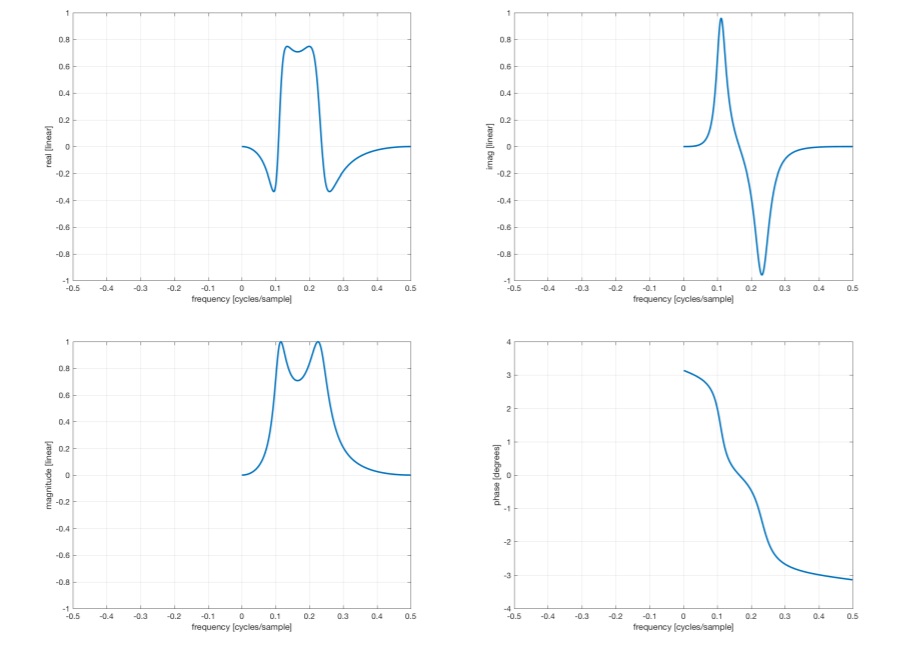
If x[n] = x*[n] is a real-valued sequence, then the DTFT X(f) has Hermitian symmetry, X() = X*(-). Decompose X(f) into its real and imaginary parts, X(f) = Xr(f) +jXi(f), (a) Prove that the real part is even, Xr(f) = X(-). X.(f) = jX()+X*()] X; (f) = {x () x* ()] (b) Prove that the imaginary part is odd, X; (f) = -X(f). (c) Prove that the magnitude is even, |X()| = |X(-)|. (d) Prove that the phase is odd, X() = ZX(). (e) For real sequences x[n], explain why it is sufficient to visualize the DTFT X(f) for only positive frequencies, 0f0.5. (f) Suppose x[n] is real and consider the partial plots of Xr(f), Xi(f), |X()\, and ZX() for 0 < < 0.5 shown below. Given the symmetry requirements on X(f), sketch the real part, imaginary, part, magnitude, and phase for -0.5 < x < 0. magnitude (linear] real (linear] 0.8 1 0.6 0.4 0.2 0 -0.2 -0.4- -0.6 -0.8 -1 0.8 1 0.6 0.4 0.2 20 0 -0.2 -0.4 -0.6 -0.8 -0.5 -1 -0.5 -0.4 -0.3 -0.2 -0.1 0 -0.4 -0.3 imag [linear] 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 0.1 0.2 0.3 0.4 0.5 -0.5 -0.4 -0.3 -0.2 -0.1 0 frequency [cycles/sample] M phase [degrees] 3 2 -2 -3 0.1 0.2 0.3 0.4 0.5 frequency (cycles/sample] -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5 -0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5 frequency [cycles/sample] frequency (cycles/sample]