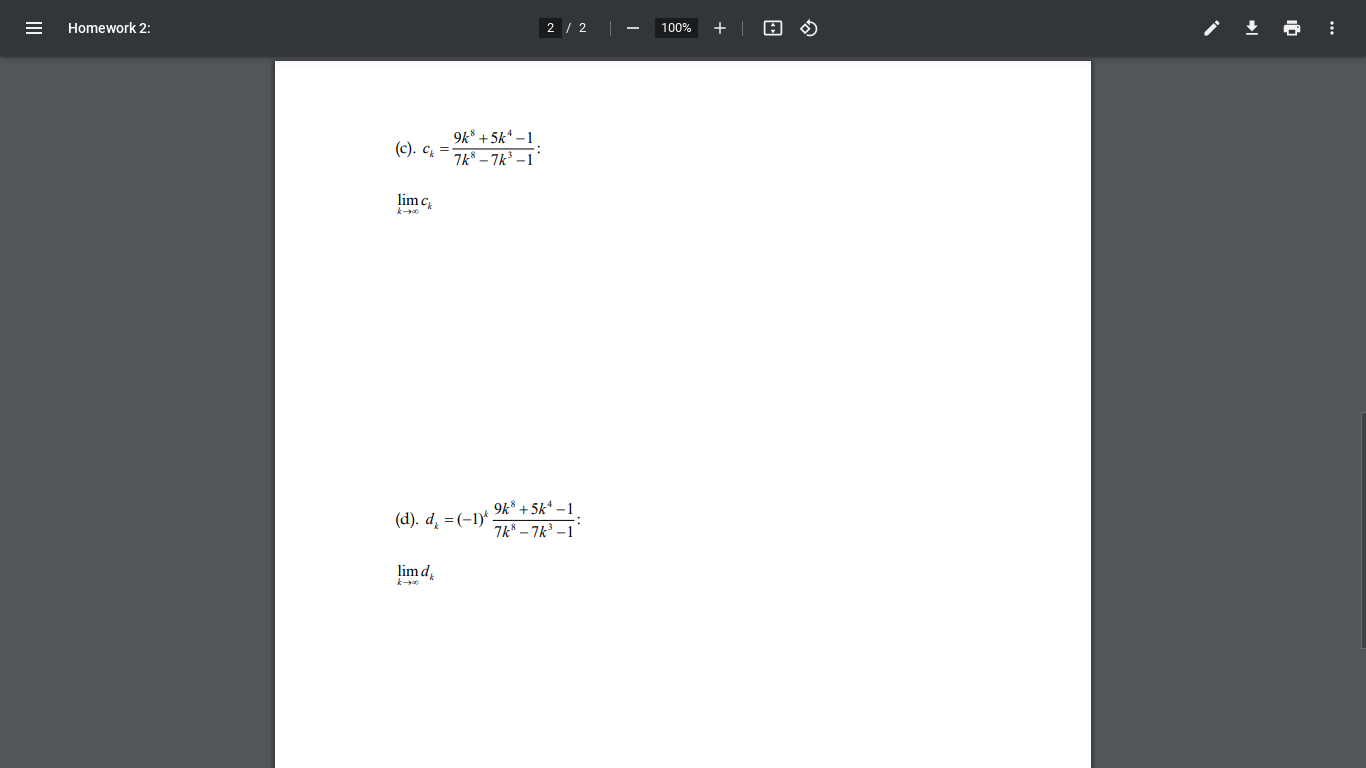
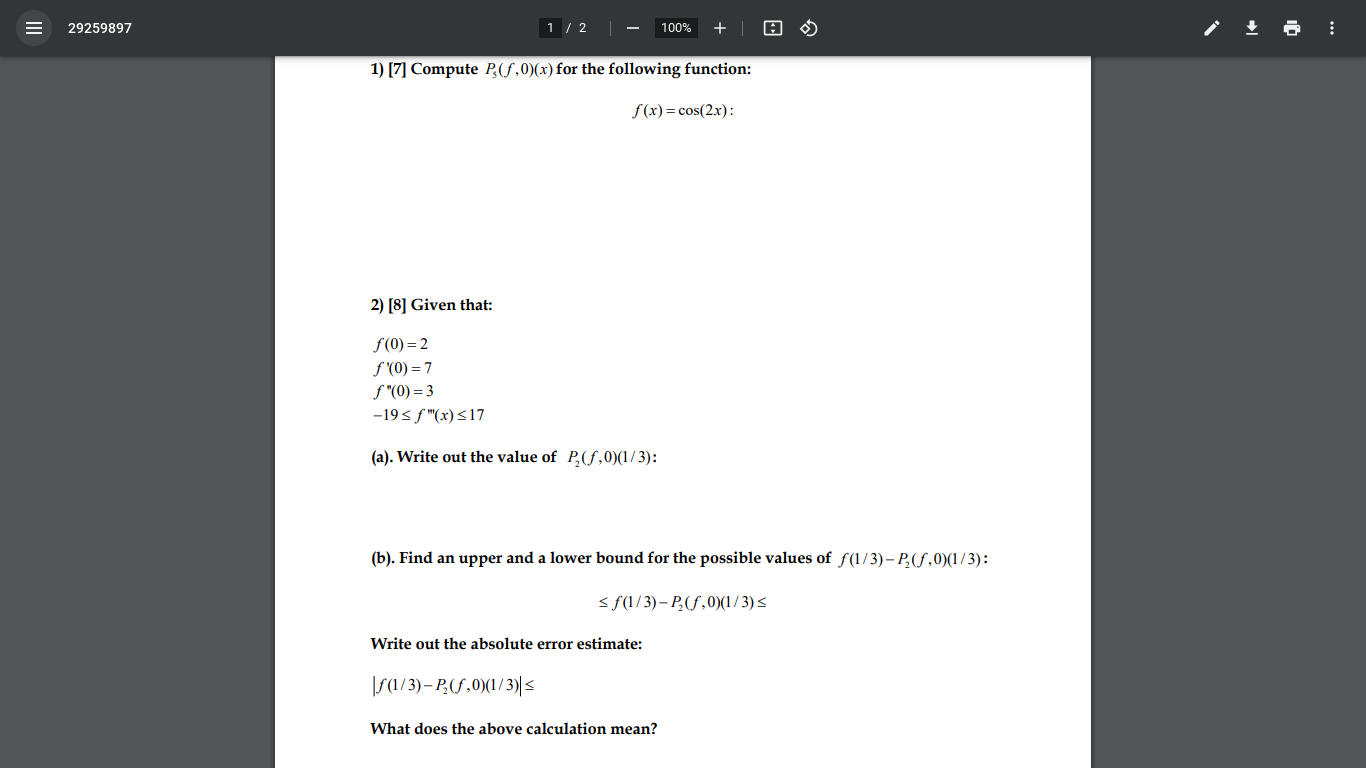
III Homework 2: 1/2 100% + 1) [24] Compute the values of the limits of the following sequences or state that the limit of the sequence does not exist. Write some justification for your assertions: (a). ak 5k 5.001-37k 1917 lim ak (b). b =(-1). 5k 5.001-37k lim b ko 1917 III Homework 2: 2 / 2 100% 9k8+5k4-1 (c). Ck 7k8-7k-1 lim Ck k-00 9k+5k4- 7k8-7k-1 : (d). d=(-1). lim d 004-3 III 29259897 1/2 100% + 1) [7] Compute P(f,0)(x) for the following function: 2) [8] Given that: f(0)=2 f'(0)=7 "(0)=3 f(x)= cos(2x): -19f"(x) 17 (a). Write out the value of P(f,0)(1/3): (b). Find an upper and a lower bound for the possible values of f(1/3)-P(,0)(1/3): f(1/3)-P(f,0)(1/3) Write out the absolute error estimate: (1/3)-Pf,0(1/3) What does the above calculation mean? III 29259897 2 / 2 100% + (c). Find an upper and a lower bound for the possible values of f(1/3): f(1/3) What does the above calculation, coupled with the calculation in part (b), mean? 3) [20] Approximate f(1/20) to within 1/100, using Taylor Polynomials centered at zero, for the function: Note: -1cos(t)1 f(x) = cos(10x). and -1sin(t) 1. You MUST write down the error estimates for all of the Taylor Polynomials starting with degree zero until you get to the one which is with error estimate less than 1/100. You MUST write down the value of the sufficiently close Taylor Polynomial.