I'm unsure how to set up a dynamic programming solution for the following problem meeting the specified time complexity:

Assume 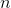houses 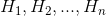are located (in this order) along a straight road. We treat the road as the real line, such that every point has a real number as coordinate. Let 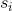denote the point where house 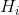is located; note that 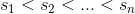. A vehicle stands at some point at time 0. The vehicle must visit all houses. However, every house 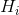must be visited before some individual deadline 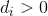. Nothing special is assumed about these deadlines. The vehicle can drive at maximum speed 1, that is, at most one length unit per time unit. (We assume distances are large, such that we neglect acceleration, deceleration and time stopped at the house. That is velocity can change instantly, and visits cost no time.)

A problem instance is given by the numbers 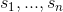, 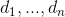and . A solution computes a route for the vehicle such that every house 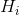is visited before .

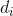Beware: It is in general not enough to first visit all houses to the left of , and then all houses to the right, or vice versa. It may be the case that customers with close deadlines await on both sides of . A complicated zigzag route may be needed. You can hardly avoid dynamic programming for this problem.

Aim for an algorithm whose time complexity is merely polynomial in 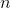, regardless of the numbers 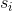and .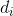

H1, H2, ...,HM S1 o S1.Sn di .... dn