Implement part two and three and do not use Java priority queue.

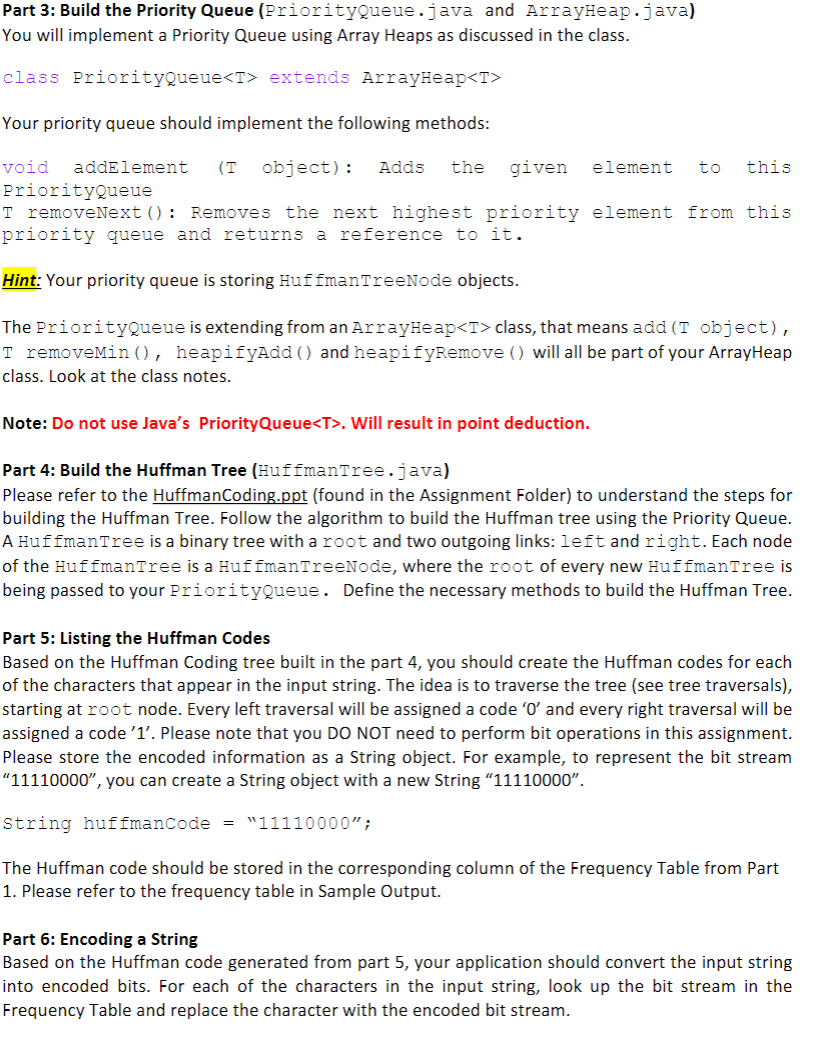
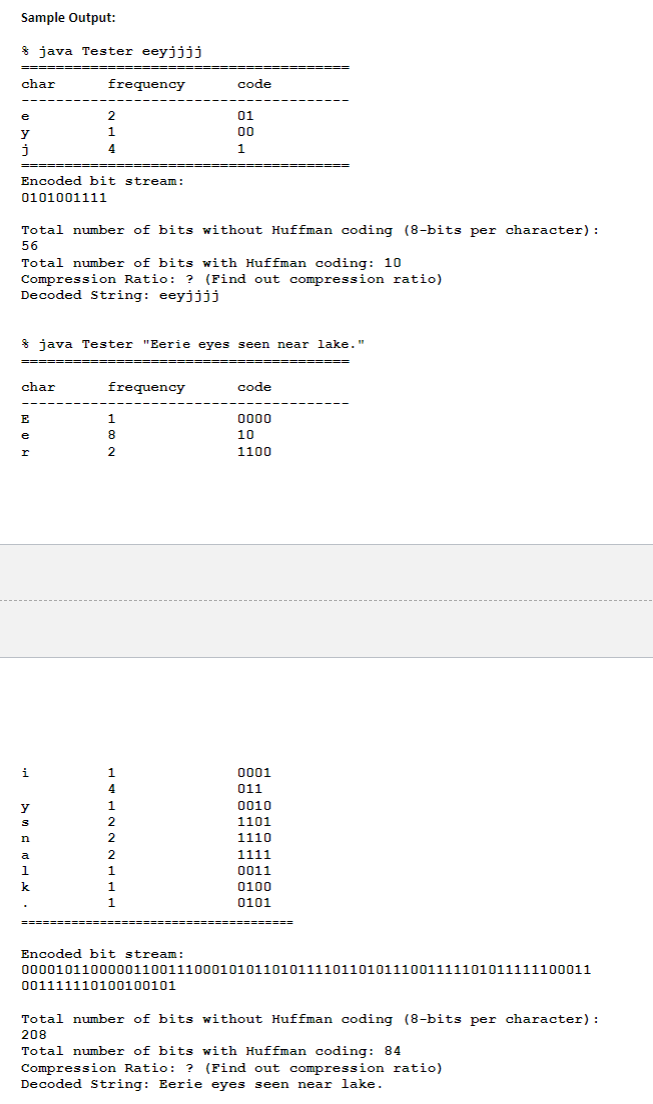
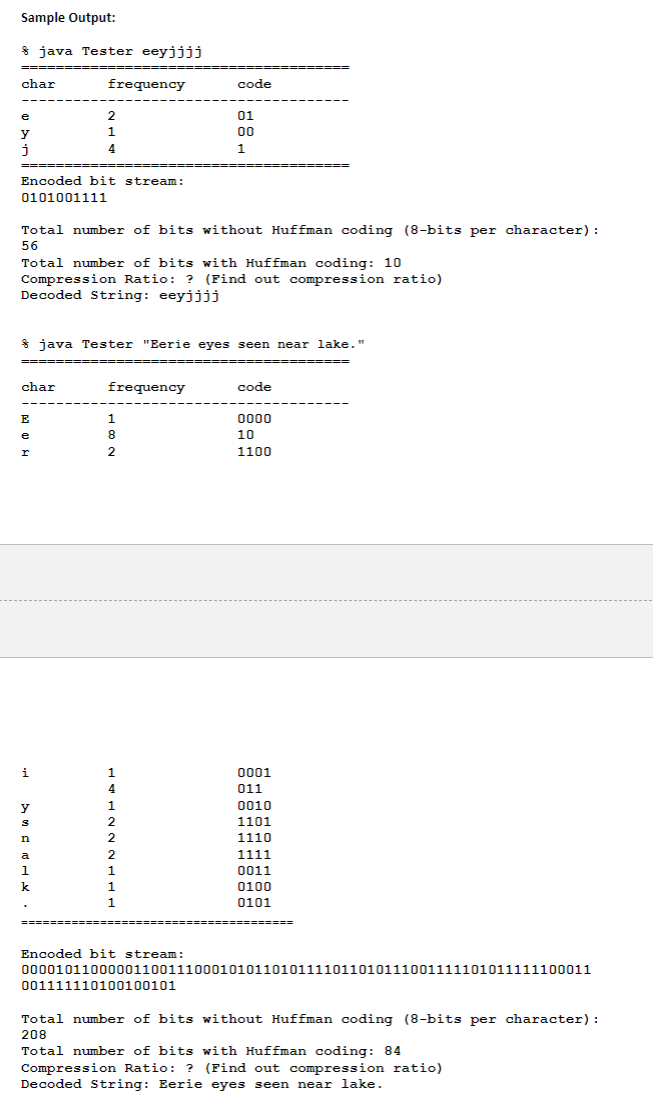
Huffman Coding: Huffman coding is an algorithm devised by David A. Huffman of MIT in 1952 for compressing text data to make a file occupy a smaller number of bytes. This relatively simple compression algorithm is powerful enough that variations of it are still used today in computer networks, fax machines, modems, HDTV, and other areas. Normally text data is stored in a standard format of 8 bits per character, commonly using an encoding called ASCII that maps every character to a binary integer value from 0-255. The idea of Huffman coding is to abandon the rigid 8-bits-percharacter requirement and use different-length binary encodings for different characters. The advantage of doing this is that if a character occurs frequently in the file, such as the letter 'e', it could be given a shorter encoding (fewer bits), making the file smaller. The tradeoff is that some characters may need to use encodings that are longer than 8 bits, but this is reserved for characters that occur infrequently, so the extra cost is worth it. Compressing Data using Huffman Coding: Part 1: Build a Frequency Table (HuffmanFrequencyTable.java) The first task is to build a frequency table. Please refer to the frequency table in Sample Output. At this point, you should fill the first two columns of this table: Character and Frequency. The Huffman code is not known yet. In this table: 1. Items include characters that appear only in the input string. 2. Characters are case sensitive 3. Characters are listed in the order of appearance in the input string 4. The minimum number of characters is 2 5. The frequency refers to the number of appearances of the character. You do not need to normalize this number. Part 2: Build a Huffman Tree Node (HuffmanTreeNode.java) Your basic building block is a Huffman Tree Node. Each node consists of an element (i.e. character from your frequency table) and a priority value (i.e. character frequency from the frequency table). Apart from the necessary get() and set() methods, your class should also implement the compareto () method: /* Returns the 1 if the current node has higher priority than the given node and -1 otherwise. / int compareTo (HuffmanTreeNode obj) Part 3: Build the Priority Queue (PriorityQueue.java and ArrayHeap.java) You will implement a Priority Queue using Array Heaps as discussed in the class. class PriorityQueue extends ArrayHeap Your priority queue should implement the following methods: void addElement (T object): Adds the given element to this PriorityQueue T removeNext(): Removes the next highest priority element from this priority queue and returns a reference to it. Hint: Your priority queue is storing HuffmanTreeNode objects. The Priorityqueue is extending from an ArrayHeap class, that means add (T object), T removeMin(), heapifyAdd() and heapifyRemove () will all be part of your ArrayHeap class. Look at the class notes. Note: Do not use Java's Priority Queue. Will result in point deduction. Part 4: Build the Huffman Tree (HuffmanTree.java) Please refer to the HuffmanCoding.ppt (found in the Assignment Folder) to understand the steps for building the Huffman Tree. Follow the algorithm to build the Huffman tree using the Priority Queue. A HuffmanTree is a binary tree with a root and two outgoing links: left and right. Each node of the HuffmanTree is a HuffmanTreeNode, where the root of every new HuffmanTree is being passed to your Priorityqueue. Define the necessary methods to build the Huffman Tree. Part 5: Listing the Huffman Codes Based on the Huffman Coding tree built in the part 4, you should create the Huffman codes for each of the characters that appear in the input string. The idea is to traverse the tree (see tree traversals), starting at root node. Every left traversal will be assigned a code 'O' and every right traversal will be assigned a code 'l'. Please note that you DO NOT need to perform bit operations in this assignment. Please store the encoded information as a String object. For example, to represent the bit stream "11110000, you can create a String object with a new String 11110000". String huffmancode = "11110000"; The Huffman code should be stored in the corresponding column of the Frequency Table from Part 1. Please refer to the frequency table in Sample Output. Part 6: Encoding a String Based on the Huffman code generated from part 5, your application should convert the input string into encoded bits. For each of the characters in the input string, look up the bit stream in the Frequency Table and replace the character with the encoded bit stream. Sample Output: * java Tester eeyjjjj char frequency code 01 00 1 Encoded bit stream: 0101001111 Total number of bits without Huffman coding (8-bits per character): 56 Total number of bits with Huffman coding: 10 Compression Ratio: ? (Find out compression ratio) Decoded String: eeyjjjj java Tester "Eerie eyes seen near lake." char frequency code E e 8 2 0000 10 1100 i 0001 011 0010 1101 1110 1111 0011 0100 0101 Encoded bit stream: 000010110000011001110001010110101111011010111001111101011111100011 001111110100100101 Total number of bits without Huffman coding (8-bits per character): 208 Total number of bits with Huffman coding: 84 Compression Ratio: ? (Find out compression ratio) Decoded String: Eerie eyes seen near lake