Implement Randomized Hill Climbing and apply it to a minimization problem involving the following function f:

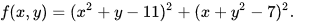
with x,y[-6,+6]

Your procedure should be called RHC and have the following input parameters:

sp: is the starting point of the Randomized Hill Climbing run

p the number of neighbors of the current solution that will be generated

z neighborhood size; for example if z is set to z=0.5 p neighbors for the current solution s are generated by adding vectors v=(z1,z2) with z1 and z2 being random numbers in [-0.5,+0.5] uniformly distributed

seed which is an integer that will be used as the seed for the random generator you employ in your implementation.

RHC returns a vector (x,y) the value of f(x,y) and the number solutions that were generated during the run of RHC.

Run your randomized hill climbing procedure RHC twice for the following parameters:

sp= (2.9, 3.2), (-2.5,+3.2), (4.2,-2) and (0,0)

p= 30 and 120

z= 0.03 and r=0.1

For each of the 32 runs report:

a. the best solution (x,y) found and its value for f

b. number of solutions generated during the run .

Summarize your results in 4 tables; one for each p and z combination . Interpret the obtained results evaluating solution quality, algorithm speed, impact of sp, p, and z on solution quality and algorithm speed. Do you believe with other values for p and r better results could be accomplished? At last, assess if RHC did a good, medium or bad job in computing a (local) minimum for f. Finally, produce one more run using sp=(4.2,-2)the 33th run by choosing parameters for p, r and seed of your own liking and report the solution s found, its value for f(s), and the number solutions searched. Solutions reported for the 33th run that are better will receive more credit.