1. Implement the algorithm maxArray, discussed in Section 2.4.3, as a C++ function. What other recursive definitions of maxArray can you describe?

2. Make sure the following requirements are met.

3. Program must compile and run.
4. maxArray function must be a recursive template function.
5. Add a main function to test the maxArray function so that you have a complete program.
6. Test the maxArray function on two arrays of different types.
7. 

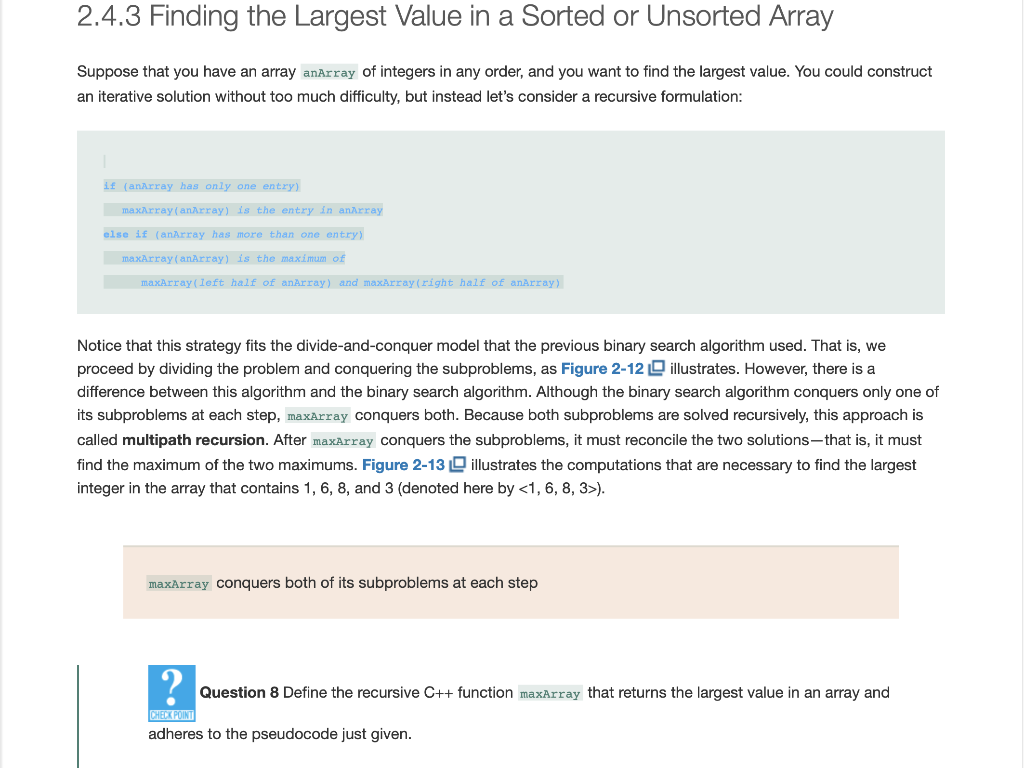
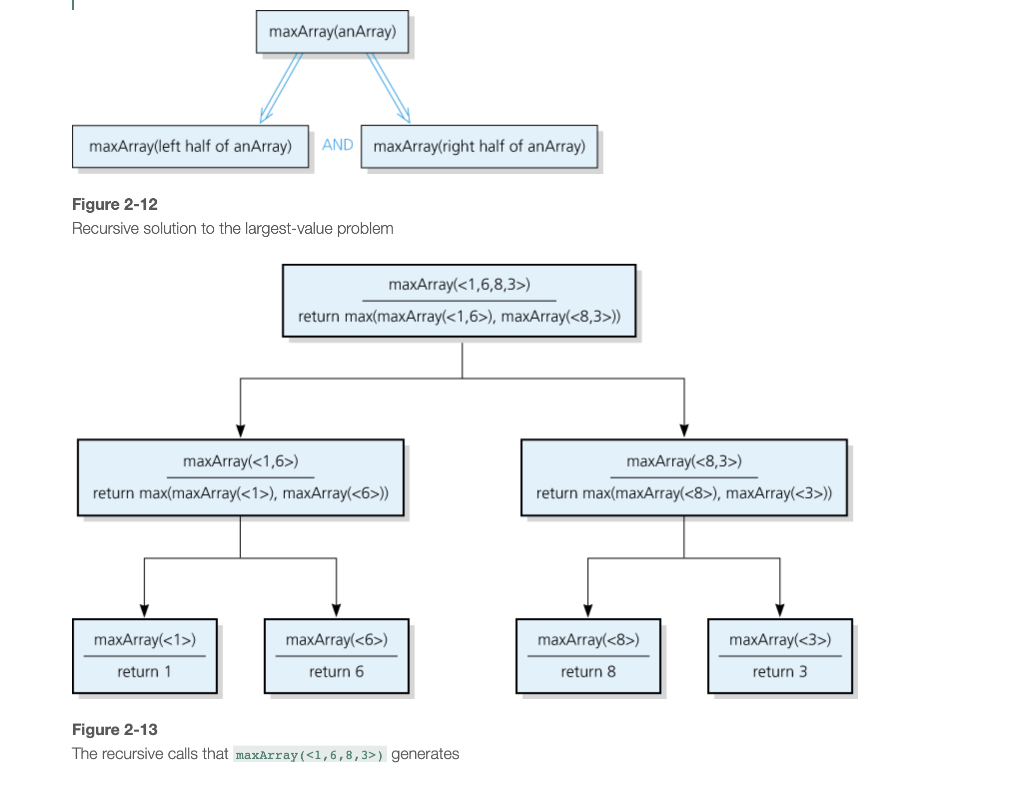
2.4.3 Finding the Largest Value in a Sorted or Unsorted Array Suppose that you have an array anArray of integers in any order, and you want to find the largest value. You could construct an iterative solution without too much difficulty, but instead let's consider a recursive formulation: if (anArray has only one entry) maxarray(anArray) is the entry in anArray else if (anArray has more than one entry) maxArray(anArray) is the maximum of maxArray (left half of anArray) and maxArray (right half of anArray) Notice that this strategy fits the divide-and-conquer model that the previous binary search algorithm used. That is, we proceed by dividing the problem and conquering the subproblems, as Figure 2-12 illustrates. However, there is a difference between this algorithm and the binary search algorithm. Although the binary search algorithm conquers only one of its subproblems at each step, maxArray conquers both. Because both subproblems are solved recursively, this approach is called multipath recursion. After maxArray conquers the subproblems, it must reconcile the two solutionsthat is, it must find the maximum of the two maximums. Figure 2-13 illustrates the computations that are necessary to find the largest integer in the array that contains 1, 6, 8, and 3 (denoted here by ). maxArray conquers both of its subproblems at each step Question 8 Define the recursive C++ function maxArray that returns the largest value in an array and CHECK POINT adheres to the pseudocode just given. maxArray(anArray) maxArray(left half of anArray) AND maxArray(right half of anArray) Figure 2-12 Recursive solution to the largest-value problem maxArray() return max(maxArray(), maxArray()) maxArray() return max(maxArray(), maxArray()) maxArray() return max(maxArray(), maxArray()) maxArray() maxArray() return 1 maxArray() return 6 maxArray() return 3 return 8 Figure 2-13 The recursive calls that maxArray () generates