Implement the algorithm shown below into a MATLAB function.

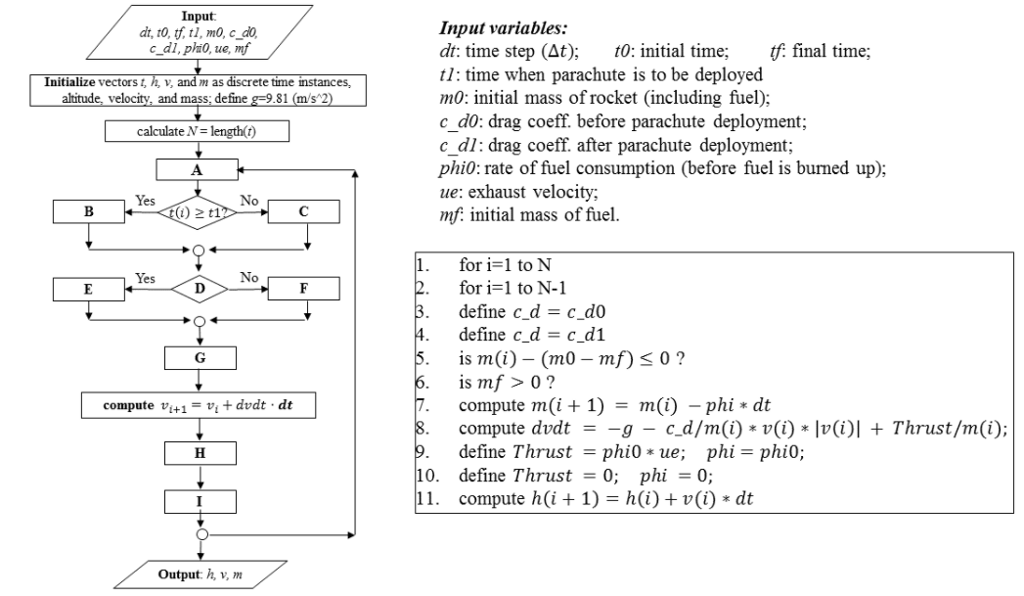
The algorithm steps is: A = 6; B = 4; C = 3; D = 5; E = 9; F = 10; G = 7; H = 8; I = 11

CODE:

function [h, v, m] = RocketTrajectory(dt, t0, tf, t1, m0, c_d0, c_d1, mfdot0, ue, mf) % Input % dt: time step (scalar) % t0: initial time (scalar) % tf: final time (scalar) % t1: time when parachute is to be deployed (scalar) % m0: initial mass of rocket including fuel (scalar) % c_d0: drag coefficient before parachute deployment (scalar) % c_d1: drag coefficient after parachute deployment (scalar) % mfdot0: fuel mass flow rate (before fuel is burned up) (scalar) % ue: exhaust velocity (scalar) % mf: initial mass of fuel (scalar) % Output % h: time history of rocket altitude from t0 to tf (1 x N vector) % v: time history of rocket velocity from t0 to tf (1 x N vector) % m: time history of rocket mass from t0 to tf (1 x N vector) % -------------------------

% Initialization t = t0:dt:tf; % define the time vector: from t0 to tf with increment dt. h = zeros(size(t)); h(1) = 0.0; % initial altitude of rocket is 0.0 v = zeros(size(t)); v(1) = 0.0; % initial velocity of rocket is 0.0 m = zeros(size(t)); m(1) = m0; % initial mass of the rocket is given as input: m0. g = 9.81; % gravitational acceleration (m/s^2)

% calculate N: dimension of vector t N = numel(t);

%Write your function here.

calculate N = length(t)

mf>0 for t(i) >= t1; c_d = c_d1 else c_d = c_d0 compute m(i) - (m0-mf)

Thank you!

Input Input variables: dt: time step (At); tO: initial time; final time; t1: time when parachute is to be deployed m0: initial mass of rocket (including fuel); c d0: drag coeff. before parachute deployment c dl: drag coeff. after parachute deployment phi0: rate of fuel consumption (before fuel is burned up); ue: exhaust velocity; mf initial mass of fuel. Initialize vectors t, h, v, andm as discrete time instances, altitude, velocity, and mass: define g9.81 (m/s 2 calculate N-length(t) Yes 0 (1) 2 t1 for i-1 to N for i-1 to N-1 define c-d = c_d0 define c-d = c-d! is m(i) - (m0 - mf)s0? is mf > 0? compute ml(it 1) = m(1)-phi * dt compute dvdt - -g - cd/m(i) v(i) Iv(i)Thrust/m(i); define Thrust = phi0 * ue; phi = phi0; define Thrust=0; phi=0; compute h(i + 1) = h(i) + u(i) * dt es compute vtv dvdt dt 10. 11, Output: h, v, m Input Input variables: dt: time step (At); tO: initial time; final time; t1: time when parachute is to be deployed m0: initial mass of rocket (including fuel); c d0: drag coeff. before parachute deployment c dl: drag coeff. after parachute deployment phi0: rate of fuel consumption (before fuel is burned up); ue: exhaust velocity; mf initial mass of fuel. Initialize vectors t, h, v, andm as discrete time instances, altitude, velocity, and mass: define g9.81 (m/s 2 calculate N-length(t) Yes 0 (1) 2 t1 for i-1 to N for i-1 to N-1 define c-d = c_d0 define c-d = c-d! is m(i) - (m0 - mf)s0? is mf > 0? compute ml(it 1) = m(1)-phi * dt compute dvdt - -g - cd/m(i) v(i) Iv(i)Thrust/m(i); define Thrust = phi0 * ue; phi = phi0; define Thrust=0; phi=0; compute h(i + 1) = h(i) + u(i) * dt es compute vtv dvdt dt 10. 11, Output: h, v, m