Implement the decoder for a (3,6) regular LDPC code for BSC (hard decoding) and AWGN channels (soft decoding) when the information block length is k=10000. Simulate 500 blocks and obtain the prediction of the bit error rate (BER) as a function of i) The probability of error in the BSC channel (hard decision), ii) Eb/N0 in the AWGN channel (soft decision). For each case (i) and (ii) present a figure showing the prediction obtained from density evolution as well as the simulation results (results from density evolution should match simulation results very well).

You do NOT need to implement the encoder (you can assume that you are always transmitting the all-zero codeword.)

Take into account this notes

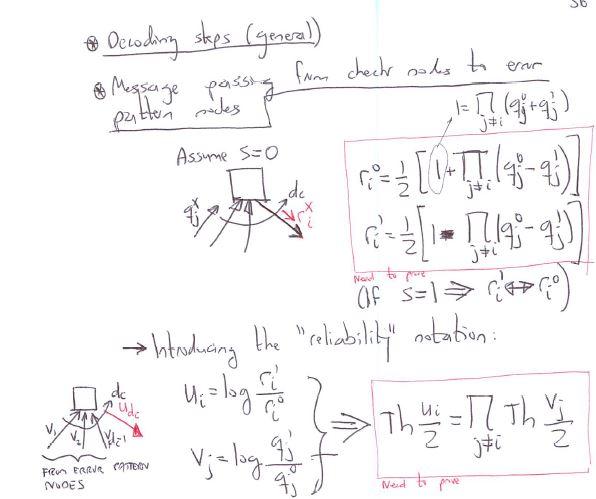
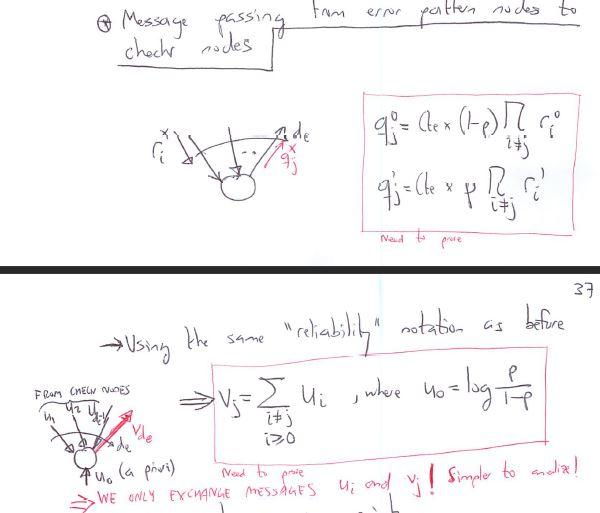
go Message passing fun chectr nolos to erar pritter sades 1=j=i(qj0+qj)ri0=21[(1+j=i(qj0qj)]ri=21[1=j=i(qj0qj)]afs=1ri1ri0) lntroduaing the "celiability" notation: ui=logri0rivj=logqjqjTh2ui=j=iTh2vj qj0=ce(1)i=jri0qj=cepi=jri Vsing the same "retiability" notation as befure \& Decision up to a given point Introducing the "reliabiliti" notation: Db=logdd0dn Dn=i=0deui, whee u0=loy1p1 Decide e^n=1 if D>0. Othervise e^n=0 Notice, reliability of a binary andum variable is defreed as Lx=log(X=0)(X=1)IfP(X=1)>P(x=0)Lx>0(ifP(X=0)>>P(X=1)Lx