implement the java program

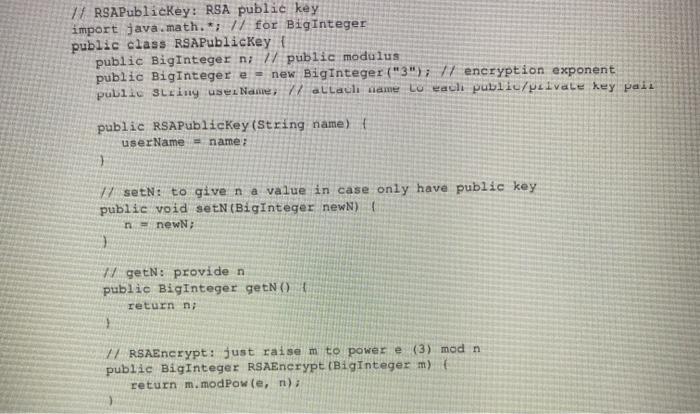
// RSAPublicKey: RSA public key import java.math.*; // for BigInteger public class RSAPublicKey { public BigInteger n; // public modulus public BigInteger e = new BigInteger ("3"); // encryption exponent public Sling use. Name, I alla li nam to each public/puivale key paid public RSAPublicKey (String name) userName = name; 1 setN: to give n a value in case only have public key public void setN(BigInteger newN) newN; W getN: provide n public BigInteger getN() return ni // RSAEncrypt: just raise m to power e (3) mod n public BigInteger RSAEncrypt (BigInteger m) { return m.modPowe, n); 1/ RSAVerify: same as encryption, since RSA is symmetric public BigInteger RSAVerify (BigInteger s) { return s.modPow(e, n); 1 // RSAPublicKey: RSA public key import java.math.*; // for BigInteger public class RSAPublicKey { public BigInteger n; // public modulus public BigInteger e = new BigInteger ("3"); // encryption exponent public Sling use. Name, I alla li nam to each public/puivale key paid public RSAPublicKey (String name) userName = name; 1 setN: to give n a value in case only have public key public void setN(BigInteger newN) newN; W getN: provide n public BigInteger getN() return ni // RSAEncrypt: just raise m to power e (3) mod n public BigInteger RSAEncrypt (BigInteger m) { return m.modPowe, n); 1/ RSAVerify: same as encryption, since RSA is symmetric public BigInteger RSAVerify (BigInteger s) { return s.modPow(e, n); 1